Different Ways of Solving a Contest Problem: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series on different ways of solving the contest problem “If $3 \sin \theta = \cos \theta$ , what is $\sin \theta \cos \theta$ ?”

Part 1: Drawing the angle $\theta$

Part 2: A first attempt using a Pythagorean identity.

Part 3: A second attempt using a Pythagorean identity and the original hypothesis for $\theta$ .

Different ways of computing a limit (Part 3)

One of my colleagues placed the following problem on an exam for his Calculus II course…

$\displaystyle \lim_{x \to \infty} \frac{\sqrt{x^2+1}}{x}$

and was impressed by the variety of correct responses that he received. I thought it would be fun to discuss some of the different ways that this limit can be computed.

Method #3. A trigonometric identity. When we see $\sqrt{x^2+1}$ inside of an integral, one kneejerk reaction is to try the trigonometric substitution $x = \tan \theta$ . So let’s use this here. Also, since $x \to \infty$ , we can change the limit to be $\theta \to \pi/2$ :

$\displaystyle \lim_{x \to \infty} \frac{\sqrt{x^2+1}}{x} = \displaystyle \lim_{\theta \to \pi/2} \frac{\sqrt{\tan^2 \theta+1}}{\tan \theta}$

$= \displaystyle \lim_{\theta \to \pi/2} \frac{\sqrt{\sec^2 \theta}}{\tan \theta}$

$= \displaystyle \lim_{\theta \to \pi/2} \frac{ \sec \theta}{\tan \theta}$

$= \displaystyle \lim_{\theta \to \pi/2} \frac{ ~~\displaystyle \frac{1}{\cos \theta} ~~}{ ~~ \displaystyle \frac{\sin \theta}{\cos \theta} ~~ }$

$= \displaystyle \lim_{\theta \to \pi/2} \frac{ 1}{\sin \theta}$

$= 1$ .

Different ways of solving a contest problem (Part 1)

The following problem appeared on the American High School Mathematics Examination (now called the AMC 12) in 1988:

If $3 \sin \theta = \cos \theta$ , what is $\sin \theta \cos \theta$ ?

When I presented this problem to a group of students, I was pleasantly surprised by the amount of creativity shown when solving this problem.

Here’s the first solution that I received: draw the appropriate triangles for the angle $\theta$ :

$3 \sin \theta = \cos \theta$

$\tan \theta = \displaystyle \frac{1}{3}$

Therefore, the angle $\theta$ must lie in either the first or third quadrant, as shown. (Of course, $\theta$ could be coterminal with either displayed angle, but that wouldn’t affect the values of $\sin \theta$ or $\cos \theta$ .)

In Quadrant I, $\sin \theta = \displaystyle \frac{1}{\sqrt{10}}$ and $\cos \theta = \displaystyle \frac{3}{\sqrt{10}}$ . Therefore,

$\sin \theta \cos \theta = \displaystyle \frac{1}{\sqrt{10}} \times \frac{3}{\sqrt{10}} = \displaystyle \frac{3}{10}$ .

In Quadrant III, $\sin \theta = \displaystyle -\frac{1}{\sqrt{10}}$ and $\cos \theta = -\displaystyle \frac{3}{\sqrt{10}}$ . Therefore,

$\sin \theta \cos \theta = \displaystyle \left( - \frac{1}{\sqrt{10}} \right) \times \left( -\frac{3}{\sqrt{10}} \right) = \displaystyle \frac{3}{10}$ .

Either way, we can be certain that $\sin \theta \cos \theta = \displaystyle \frac{3}{10}$ .

How I Impressed My Wife: Part 5b

Amazingly, the integral below has a simple solution:

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x} = \displaystyle \frac{2\pi}{|b|}.$

Even more amazingly, the integral $Q$ ultimately does not depend on the parameter $a$ . For several hours, I tried to figure out a way to demonstrate that $Q$ is independent of $a$ , but I couldn’t figure out a way to do this without substantially simplifying the integral, but I’ve been unable to do so (at least so far).

So here’s what I have been able to develop to prove that $Q$ is independent of $a$ without directly computing the integral $Q$ .

Earlier in this series, I showed that

$Q = 2 \displaystyle \int_{-\pi/2}^{\pi/2} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x}$

$= 2 \displaystyle \int_{-\pi/2}^{\pi/2} \frac{\sec^2 x dx}{1 + 2 a \tan x + (a^2 + b^2) \tan^2 x}$

$= 2 \displaystyle \int_{-\infty}^{\infty} \frac{du}{1 + 2 a u + (a^2+b^2) u^2}$

$= \displaystyle \frac{2}{a^2+b^2} \int_{-\infty}^{\infty} \frac{dv}{v^2 + \displaystyle \frac{b^2}{(a^2+b^2)^2} }$

$= \displaystyle 2 \int_{-\infty}^{\infty} \frac{(a^2+ b^2) dv}{(a^2 + b^2) v^2 + b^2 }$

Yesterday, I showed used the substitution $w = (a^2 + b^2) v$ to show that $Q$ was independent of $a$ . Today, I’ll use a different method to establish the same result. Let

$Q(a) = \displaystyle 2 \int_{-\infty}^{\infty} \frac{(a^2+b^2) dv}{(a^2+b^2)^2 v^2 + b^2 }$ .

Notice that I’ve written this integral as a function of the parameter $a$ . I will demonstrate that $Q'(a) = 0$ , so that $Q(c)$ is a constant with respect to $a$ . In other words, $Q(a)$ does not depend on $a$ .

To do this, I differentiate under the integral sign with respect to $a$ (as opposed to $x$ ) using the Quotient Rule:

$Q'(a) = \displaystyle 2 \int_{-\infty}^{\infty} \frac{ 2a \left[ (a^2+b^2)^2 v^2 + b^2\right] - 2 (a^2+b^2) \cdot (a^2+b^2) v^2 \cdot 2a }{\left[ (a^2+b^2)^2 v^2 + b^2 \right]^2} dv$

$Q'(a) = \displaystyle 4a \int_{-\infty}^{\infty} \frac{(a^2+b^2)^2 v^2 + b^2- 2 (a^2+b^2)^2 v^2}{\left[ (a^2+b^2)^2 v^2 + b^2 \right]^2} dv$

$Q'(a) = \displaystyle 4a \int_{-\infty}^{\infty} \frac{b^2-(a^2+b^2)^2 v^2}{\left[ (a^2+b^2)^2 v^2 + b^2 \right]^2} dv$

I now apply the trigonometric substitution $v = \displaystyle \frac{b}{a^2+b^2} \tan \theta$ , so that

$(a^2+b^2)^2 v^2 = (a^2+b^2)^2 \displaystyle \left[ \frac{b}{a^2+b^2} \tan \theta \right]^2 = b^2 \tan^2 \theta$

and

$dv = \displaystyle \frac{b}{a^2+b^2} \sec^2 \theta \, d\theta$

The endpoints of integration change from $-\infty < v < \infty$ to $-\pi/2 < \theta < \pi/2$ , and so

$Q'(a) = \displaystyle 4a \int_{-\pi/2}^{\pi/2} \frac{b^2- b^2 \tan^2 \theta}{\left[ b^2 \tan^2 \theta + b^2 \right]^2} \frac{b}{a^2+b^2} \sec^2 \theta \, d\theta$

$= \displaystyle \frac{4ab^3}{a^2+b^2} \int_{-\pi/2}^{\pi/2} \frac{[1- \tan^2 \theta] \sec^2 \theta}{\left[ \tan^2 \theta +1 \right]^2} d\theta$

$= \displaystyle \frac{4ab^3}{a^2+b^2} \int_{-\pi/2}^{\pi/2} \frac{[1-\tan^2 \theta] \sec^2 \theta}{\left[ \sec^2 \theta \right]^2} d\theta$

$= \displaystyle \frac{4ab^3}{a^2+b^2} \int_{-\pi/2}^{\pi/2} \frac{[1-\tan^2 \theta] \sec^2 \theta}{\sec^4 \theta} d\theta$

$= \displaystyle \frac{4ab^3}{a^2+b^2} \int_{-\pi/2}^{\pi/2} \frac{[1- \tan^2 \theta]}{\sec^2 \theta} d\theta$

$= \displaystyle \frac{4ab^3}{a^2+b^2} \int_{-\pi/2}^{\pi/2} [1- \tan^2 \theta] \cos^2 \theta \, d\theta$

$= \displaystyle \frac{4ab^3}{a^2+b^2} \int_{-\pi/2}^{\pi/2} [\cos^2 \theta -\sin^2 \theta] d\theta$

$= \displaystyle \frac{4ab^3}{a^2+b^2} \int_{-\pi/2}^{\pi/2} \cos 2\theta \, d\theta$

$= \displaystyle \left[ \frac{2ab^3}{a^2+b^2} \sin 2\theta \right]^{\pi/2}_{-\pi/2}$

$= \displaystyle \frac{2ab^3}{a^2+b^2} \left[ \sin \pi - \sin (-\pi) \right]$

$= \displaystyle \frac{2ab^3}{a^2+b^2} \left[ 0- 0 \right]$

$= 0$ .

I’m not completely thrilled with this demonstration that $Q$ is independent of $a$ , mostly because I had to do so much simplification of the integral $Q$ to get this result. As I mentioned in yesterday’s post, I’d love to figure out a way to directly start with

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x}$

and demonstrate that $Q$ is independent of $a$ , perhaps by differentiating $Q$ with respect to $a$ and demonstrating that the resulting integral must be equal to 0. However, despite several hours of trying, I’ve not been able to establish this result without simplifying $Q$ first.

How I Impressed My Wife: Part 3f

Previously in this series, I showed that

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x} = \displaystyle \frac{2\pi}{|b|}.$

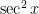
My wife had asked me to compute this integral by hand because Mathematica 4 and Mathematica 8 gave different answers. At the time, I eventually obtained the solution by multiplying the top and bottom of the integrand by $\sec^2 x$ and then employing the substitution $u = \tan x$ (after using trig identities to adjust the limits of integration).

But this wasn’t the only method I tried. Indeed, I tried two or three different methods before deciding they were too messy and trying something different. So, for the rest of this series, I’d like to explore different ways that the above integral can be computed.

So far, I have shown that

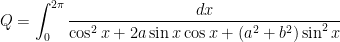
$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x}$

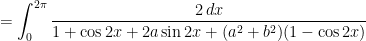
$= \displaystyle \int_0^{2\pi} \frac{2 \, dx}{1+\cos 2x + 2 a \sin 2x + (a^2 + b^2)(1-\cos 2x)}$

$= 2 \displaystyle \int_0^{2\pi} \frac{d\theta}{(1+a^2+b^2) + 2 a \sin \theta + (1 - a^2 - b^2) \cos \theta}$

$= 2 \displaystyle \int_{0}^{2\pi} \frac{d\theta}{S + R \cos (\theta - \alpha)}$

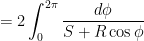
$= 2 \displaystyle \int_{0}^{2\pi} \frac{d\phi}{S + R \cos \phi}$

$= 2 \displaystyle \int_{-\pi}^{\pi} \frac{d\phi}{S + R \cos \phi}$

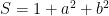where $R = \sqrt{(2a)^2 + (1-a^2-b^2)^2}$ and $S = 1 + a^2 + b^2$ (and $\alpha$ is a certain angle that is now irrelevant at this point in the calculation).

There are actually a couple of ways for computing this last integral. Today, I’ll lay the foundation for the “magic substitution”

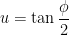
$u = \tan \displaystyle \frac{\phi}{2}$

With this substitution, the above integral will become a rational function, which can then be found using standard techniques.

First, we use some trig identities to rewrite $\cos 2x$ in terms of $\tan x$ :

$\cos 2x = 2\cos^2 x - 1$

$= \displaystyle \frac{ \sec^2 x (2 \cos^2 x - 1)}{\sec^2 x}$

$= \displaystyle \frac{ 2 - \sec^2 x)}{\sec^2 x}$

$= \displaystyle \frac{ 2 - [ 1 + \tan^2 x])}{1 + \tan^2 x}$

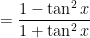
$= \displaystyle \frac{1- \tan^2 x}{1 + \tan^2 x}$

Next, I’ll replace $x$ by $\phi/2$ :

$\cos \phi = \displaystyle \frac{1- \tan^2 (\phi/2)}{1 + \tan^2 (\phi/2)} = \displaystyle \frac{1-u^2}{1+u^2}$ .

Second, for the sake of completeness (even though it isn’t necessary for this particular integral), I’ll rewrite $\sin 2x$ in terms of $\tan x$ :

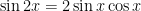
$\sin 2x = 2\sin x \cos x$

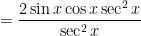
$= \displaystyle \frac{2\sin x \cos x \sec^2 x}{\sec^2 x}$

$= \displaystyle \frac{ ~ \displaystyle \frac{2 \sin x}{\cos x} ~ }{\sec^2 x}$

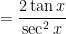
$= \displaystyle \frac{ 2 \tan x }{\sec^2 x}$

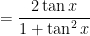
$= \displaystyle \frac{ 2 \tan x }{1 + \tan^2 x}$

$= \displaystyle \frac{2 \tan x}{1 + \tan^2 x}$

Next, I’ll replace $x$ by $\phi/2$ :

$\sin \phi = \displaystyle \frac{2 \tan^2 (\phi/2)}{1 + \tan^2 (\phi/2)} = \displaystyle \frac{2u}{1+u^2}$ .

Third, again for the sake of completeness,

$\tan \phi = \displaystyle \frac{\sin u}{\cos u} = \displaystyle \frac{ ~ \displaystyle \frac{2u}{1+u^2} ~ }{ ~ \displaystyle \frac{1-u^2}{1+u^2} ~ } = \displaystyle \frac{2u}{1-u^2}$ .

Finally, I need to worry about what happens to the $d\phi$ :

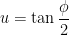
$u = \tan \displaystyle \frac{\phi}{2}$

$du = \displaystyle \frac{1}{2} \sec^2 \displaystyle \frac{\phi}{2} \, d\phi$

$du = \displaystyle \frac{1}{2} \left[ 1 + \tan^2 \displaystyle \frac{\phi}{2} \right] d\phi$

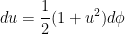
$du = \displaystyle \frac{1}{2} (1+u^2) d\phi$

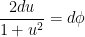
$\displaystyle \frac{2 du}{1+u^2} = d\phi$

These four substitutions can be used to convert trigonometric integrals into some other integral. Usually, the new integrand is pretty messy, and so these substitutions should only be used sparingly, as a last resort.

I’ll continue this different method of evaluating this integral in tomorrow’s post.

How I Impressed My Wife: Part 2b

Some husbands try to impress their wives by lifting extremely heavy objects or other extraordinary feats of physical prowess.

That will never happen in the Quintanilla household in a million years.

But she was impressed that I broke an impasse in her research and resolved a discrepancy between Mathematica 4 and Mathematica 8 by finding the following integral by hand in less than an hour:

$Q = \displaystyle \int_0^{2\pi} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x}$

In this series, I’ll explore different ways of evaluating this integral.In yesterday’s post, I showed that

$Q = 2 \displaystyle \int_{-\pi/2}^{\pi/2} \frac{dx}{\cos^2 x + 2 a \sin x \cos x + (a^2 + b^2) \sin^2 x}$

We now multiply the top and bottom of the integrand by $\sec^2 x$ . This is permissible because $\sec^2 x$ is defined on the interior of the interval $(-\pi/2, \pi/2)$ — which is why I needed to adjust the limits of integration in the first place. I obtain

$Q = 2 \displaystyle \int_{-\pi/2}^{\pi/2} \frac{\sec^2 x dx}{\cos^2 x \sec^2 x + 2 a \sin x \cos x \sec^2 x + (a^2 + b^2) \sin^2 x \sec^2 x}$

Next, I use some trigonometric identities to simplify the denominator:

$\cos^2 x \sec^2 x = \cos^2 x \displaystyle \frac{1}{\cos^2 x} = 1$
$\sin x \cos x \sec^2 x = \sin x \cos x \frac{1}{\cos^2 x} = \displaystyle \frac{\sin x}{\cos x} = \tan x$
$\sin^2 x \sec^2 x = \sin^2 x \displaystyle \frac{1}{\cos^2 x} = \displaystyle \left( \frac{\sin x}{\cos x} \right)^2 = \tan^2 x$

Therefore, the integral becomes

$Q = 2 \displaystyle \int_{-\pi/2}^{\pi/2} \frac{\sec^2 x dx}{1 + 2 a \tan x + (a^2 + b^2) \tan^2 x}$

I’ll continue with the evaluation of this integral in tomorrow’s post.

Tag: ratio trig identities

Different Ways of Solving a Contest Problem: Index

Different ways of computing a limit (Part 3)

Different ways of solving a contest problem (Part 1)

How I Impressed My Wife: Part 5b

How I Impressed My Wife: Part 3f

How I Impressed My Wife: Part 2b

Trig identity