Earlier in this series, I gave three different methods of showing that

Using the fact that
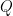
is independent of

, I’ll now give a fourth method.

Since
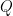
is independent of

, I can substitute any convenient value of

that I want without changing the value of
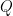
. As shown in previous posts, substituting
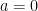
yields the following simplification:
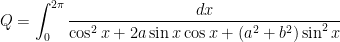
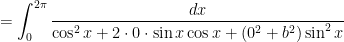



The four roots of the denominator satisfy
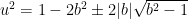
So far, I’ve handled the cases 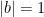 and
and 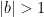 . In today’s post, I’ll start considering the case
. In today’s post, I’ll start considering the case 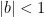 .
.
Factoring the denominator is a bit more complicated if 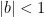 . Using the quadratic equation, we obtain
. Using the quadratic equation, we obtain

However, unlike the cases 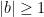 , the right-hand side is now a complex number. So, To solve for
, the right-hand side is now a complex number. So, To solve for  , I’ll use DeMoivre’s Theorem and some surprisingly convenient trig identities. Notice that
, I’ll use DeMoivre’s Theorem and some surprisingly convenient trig identities. Notice that
 .
.
Therefore, the four complex roots of the denominator satisfy  , or
, or  . This means that all four roots can be written in trigonometric form so that
. This means that all four roots can be written in trigonometric form so that
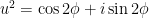 ,
,
where  is some angle. (I chose the angle to be
is some angle. (I chose the angle to be  instead of
instead of 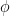 for reasons that will become clear shortly.)
for reasons that will become clear shortly.)
I’ll begin with solving
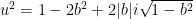 .
.
Matching the real and imaginary parts, we see that
 ,
,
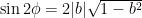
This completely matches the form of the double-angle trig identities
 ,
,
 ,
,
and so the problem reduces to solving
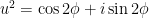 ,
,
where $\sin \phi = |b|$ and $\cos \phi = \sqrt{1-b^2}$. By De Moivre’s Theorem, I can conclude that the two solutions of this equation are
 ,
,
or
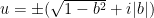 .
.
I could re-run this argument to solve  and get the other two complex roots. However, by the Conjugate Root Theorem, I know that the four complex roots of the denominator
and get the other two complex roots. However, by the Conjugate Root Theorem, I know that the four complex roots of the denominator  must come in conjugate pairs. Therefore, the four complex roots are
must come in conjugate pairs. Therefore, the four complex roots are
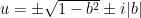 .
.
Therefore, I can factor the denominator as follows:
![u^4 + (4 b^2 - 2) u^2 + 1 = (u - [\sqrt{1-b^2} + i|b|])(u - [\sqrt{1-b^2} - i|b|])](https://s0.wp.com/latex.php?latex=u%5E4+%2B+%284+b%5E2+-+2%29+u%5E2+%2B+1+%3D+%28u+-+%5B%5Csqrt%7B1-b%5E2%7D+%2B+i%7Cb%7C%5D%29%28u+-+%5B%5Csqrt%7B1-b%5E2%7D+-+i%7Cb%7C%5D%29&bg=ffffff&fg=000000&s=0&c=20201002)
![\qquad \times (u - [-\sqrt{1-b^2} + i|b|])(u - [-\sqrt{1-b^2} + i|b|])](https://s0.wp.com/latex.php?latex=%5Cqquad+%5Ctimes+%28u+-+%5B-%5Csqrt%7B1-b%5E2%7D+%2B+i%7Cb%7C%5D%29%28u+-+%5B-%5Csqrt%7B1-b%5E2%7D+%2B+i%7Cb%7C%5D%29&bg=ffffff&fg=000000&s=0&c=20201002)
![= (u - \sqrt{1-b^2} - i|b|)(u - \sqrt{1-b^2} + i|b])](https://s0.wp.com/latex.php?latex=%3D+%28u+-+%5Csqrt%7B1-b%5E2%7D+-+i%7Cb%7C%29%28u+-+%5Csqrt%7B1-b%5E2%7D+%2B+i%7Cb%5D%29&bg=ffffff&fg=000000&s=0&c=20201002)

![= ([u - \sqrt{1-b^2}]^2 +b^2)([u + \sqrt{1-b^2}]^2 +b^2)](https://s0.wp.com/latex.php?latex=%3D+%28%5Bu+-+%5Csqrt%7B1-b%5E2%7D%5D%5E2+%2Bb%5E2%29%28%5Bu+%2B+%5Csqrt%7B1-b%5E2%7D%5D%5E2+%2Bb%5E2%29&bg=ffffff&fg=000000&s=0&c=20201002)
To double-check my work, I can directly multiply this product:
![([u - \sqrt{1-b^2}]^2 +b^2)([u + \sqrt{1-b^2}]^2 +b^2)](https://s0.wp.com/latex.php?latex=%28%5Bu+-+%5Csqrt%7B1-b%5E2%7D%5D%5E2+%2Bb%5E2%29%28%5Bu+%2B+%5Csqrt%7B1-b%5E2%7D%5D%5E2+%2Bb%5E2%29&bg=ffffff&fg=000000&s=0&c=20201002)

![= ([u^2 +1] - 2u\sqrt{1-b^2})([u^2+1] + 2u\sqrt{1-b^2})](https://s0.wp.com/latex.php?latex=%3D+%28%5Bu%5E2+%2B1%5D+-+2u%5Csqrt%7B1-b%5E2%7D%29%28%5Bu%5E2%2B1%5D+%2B+2u%5Csqrt%7B1-b%5E2%7D%29&bg=ffffff&fg=000000&s=0&c=20201002)
![= [u^2+1]^2 - [2u\sqrt{1-b^2}]^2](https://s0.wp.com/latex.php?latex=%3D+%5Bu%5E2%2B1%5D%5E2+-+%5B2u%5Csqrt%7B1-b%5E2%7D%5D%5E2&bg=ffffff&fg=000000&s=0&c=20201002)

![= u^4 + u^2 (2 - 4[1-b^2]) + 1](https://s0.wp.com/latex.php?latex=%3D+u%5E4+%2B+u%5E2+%282+-+4%5B1-b%5E2%5D%29+%2B+1&bg=ffffff&fg=000000&s=0&c=20201002)
 .
.
So, at last, I can rewrite the integral  as
as
![Q = \displaystyle \int_{-\infty}^{\infty} \frac{ 2(1+u^2) du}{ ([u - \sqrt{1-b^2}]^2 +b^2)([u + \sqrt{1-b^2}]^2 +b^2)}](https://s0.wp.com/latex.php?latex=Q+%3D+%5Cdisplaystyle+%5Cint_%7B-%5Cinfty%7D%5E%7B%5Cinfty%7D+%5Cfrac%7B+2%281%2Bu%5E2%29+du%7D%7B+%28%5Bu+-+%5Csqrt%7B1-b%5E2%7D%5D%5E2+%2Bb%5E2%29%28%5Bu+%2B+%5Csqrt%7B1-b%5E2%7D%5D%5E2+%2Bb%5E2%29%7D&bg=ffffff&fg=000000&s=0&c=20201002)

I’ll continue with this fourth evaluation of the integral, continuing the case 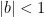 , in tomorrow’s post.
, in tomorrow’s post.
, what is
?
:
must lie in either the first or third quadrant, as shown. (Of course,
could be coterminal with either displayed angle, but that wouldn’t affect the values of
or
.)
and
. Therefore,
.
and
. Therefore,
.
.

