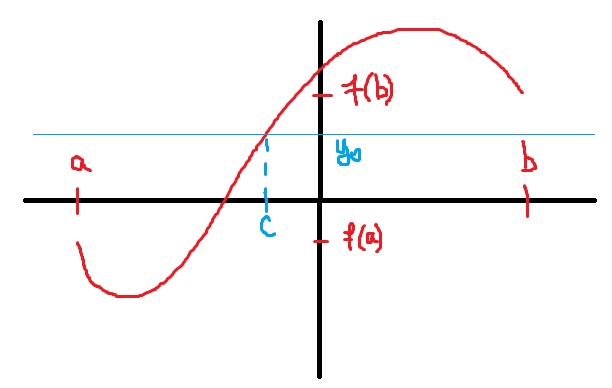
A vivid illustration of a discontinuous function

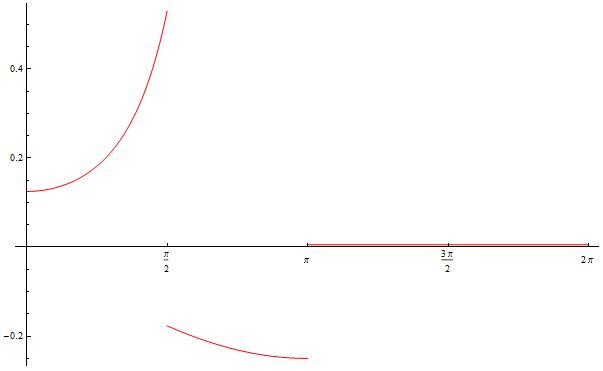
The essay Singular Limits in the May 2002 issue of Physics Today has a vivid illustration of a discontinuous function $F(x)$ which measures the ickiness one feels after eating an apple but observing that proportion $x$ of a maggot is still inside the apple. For this function, $\displaystyle \lim_{x \to 0^+} F(x) \ne F(0)$ .

Biting into an apple and finding a maggot is unpleasant enough, but finding half a maggot is worse. Discovering one-third of a maggot would be more distressing still: The less you find, the more you might have eaten. Extrapolating to the limit, an encounter with no maggot at all should be the ultimate bad-apple experience. This remorseless logic fails, however, because the limit is singular: A very small maggot fraction ( $f \ll 1$ ) is qualitatively different from no maggot ( $f=0$ ).

My Favorite One-Liners: Part 72

In this series, I’m compiling some of the quips and one-liners that I’ll use with my students to hopefully make my lessons more memorable for them.

In calculus, the Intermediate Value Theorem states that if $f$ is a continuous function on the closed interval $[a,b]$ and $y_0$ is any number between $f(a)$ and $f(b)$ , then there is at least one point $c \in [a,b]$ so that $f(c) =y_0$.

When I first teach this, I’ll draw some kind of crude diagram on the board:

In this picture, $f(a)$ is less than $y_0$ while $f(b)$ is greater than $y_0$ . Hence the one-liner:

I call the Intermediate Value Theorem the Goldilocks principle. After all, $f(a)$ is too low, and $f(b)$ is too high, but there is some point in between that is just right.

A Natural Function with Discontinuities: Index

I’m doing something that I should have done a long time ago: collecting a series of posts into one single post. The following links comprised my series on a natural function that nevertheless has discontinuities.

Part 1: Introduction

Part 2: Derivation of this piecewise function, beginning.

Part 3: Derivation of the piecewise function, ending.

A natural function with discontinuities (Part 1)

The following tidbit that was published on the American Mathematical Monthly’s Facebook page caught my attention:

Source: https://www.facebook.com/AmerMathMonthly/photos/a.250425975006394.53155.241224542593204/1021059947942989/?type=3&theater

Here’s the relationship between $r$ , $R$ , and $\theta$ in case it isn’t clear from the description. The gray sector is determined by $r$ and $\theta$ , and then the blue circle with radius $r$ is chosen to enclose the sector.

Unfortunately, there was typo for the third case; it should have been $r = R \sin \frac{1}{2} \theta$ if $90^\circ \le \theta \le 180^\circ$ . Here’s the graph if $R = 1$ , using radians instead of degrees:

As indicated in the article, there’s a discontinuity at $t=0$ . However, the rest of the graph looks nice and smooth.

Here’s the graph of the first derivative:

The first derivative is continuous (and so the original graph is smooth). However, there are obvious corners in the graph of the first derivative, which betray discontinuities in the graph of the second derivative: