Langley’s Adventitious Angles (Part 1)

Math With Bad Drawings had an interesting post about solving for $x$ in the following picture (this picture is taken from http://thinkzone.wlonk.com/MathFun/Triangle.htm):

I had never heard of this problem before, but it’s apparently well known and is called Langley’s Adventitious Angles. See Math With Bad Drawings, Wikipedia, and Math Pages for more information about the solution of this problem. Math Pages has a nice discussion about mathematical aspects of this problem, including connections to the Laws of Sines and Cosines and to various trig identities.

I’d encourage you to try to solve for $x$ without clicking on any of these links… a certain trick out of the patented Bag of Tricks is required to solve this problem using only geometry (as opposed to the Law of Cosines and the Law of Sines). I have a story that I tell my students about the patented Bag of Tricks: Socrates gave the Bag of Tricks to Plato, Plato gave it to Aristotle, it passed down the generations, my teacher taught the Bag of Tricks to me, and I teach it to my students. In the same post, Math With Bad Drawings has a nice discussion about pedagogical aspects of this problem concerning when a “trick” becomes a “technique”.

I recommend this problem for advanced geometry students who need to be challenged; even bright students will be stumped concerning coming up with the requisite trick on their own. Indeed, the problem still remains quite challenging even after the trick is shown.

Formula for an infinite geometric series (Part 10)

I conclude this series of posts by considering the formula for an infinite geometric series. Somewhat surprisingly (to students), the formula for an infinite geometric series is actually easier to remember than the formula for a finite geometric series.

One way of deriving the formula parallels the derivation for a finite geometric series. If $a_1, a_2, a_3, \dots$ are the first terms of an infinite geometric sequence, let

$S = a_1 + a_2 + a_3 + \dots$

Recalling the formula for an geometric sequence, we know that

$a_2 = a_1 r$

$a_3 = a_1 r^2$

$\vdots$

Substituting, we find

$S = a_1 + a_1 r+ a_1 r^2 \dots$

Once again, we multiply both sides by $-r$ .

$-rS = -a_1r - a_1 r^2- a_1 r^3 \dots$

Next, we add the two equations. Notice that almost everything cancels on the right-hand side… except for the leading term $a_1$ . (Unlike yesterday’s post, there is no “last” term that remains since the series is infinite.) Therefore,

$S - rS = a_1$

$S(1-r) = a_1$

$S = \displaystyle \frac{a_1}{1-r}$

A quick pedagogical note: I find that this derivation “sells” best to students when I multiply by $-r$ and add, as opposed to multiplying by $r$ and subtracting.

The above derivation is helpful for remembering the formula but glosses over an extremely important detail: not every infinite geometric series converges. For example, if $a_1 = 1$ and $r = 2$ , then the infinite geometric series becomes

$1 + 2 + 4 + 8 + 16 + \dots$ ,

which clearly does not have a finite answer. We say that this series diverges. In other words, trying to evaluate this sum makes as much sense as trying to divide a number by zero: there is no answer.

That said, it can be shown that, as long as $-1 < r < 1$ , then the above geometric series converges, so that

$a_1 + a_1 r + a_1 r^2 + \dots = \displaystyle \frac{a_1}{1-r}$

The formal proof requires the use of the formula for a finite geometric series:

$a_1 + a_1 r + a_1 r^2 + \dots + a_1 r^{n-1} = \displaystyle \frac{a_1(1-r^n)}{1-r}$

We then take the limit as $n \to \infty$ :

$\displaystyle \lim_{n \to \infty} a_1 + a_1 r + a_1 r^2 + \dots + a_1 r^{n-1} = \displaystyle \lim_{n \to \infty} \frac{a_1(1-r^n)}{1-r}$

$a_1 + a_1 r + a_1 r^2 + \dots = \displaystyle \lim_{n \to \infty} \frac{a_1(1-r^n)}{1-r}$

On the right-hand side, the only piece that contains an $n$ is the term $r^n$ . If $-1 < r < 1$ , then $r^n \to 0$ as $n \to \infty$ . (This limit fails, however, if $r \ge 1$ or $r \le -1$ .) Therefore,

$a_1 + a_1 r + a_1 r^2 + \dots = \displaystyle \lim_{n \to \infty} \frac{a_1(1-0)}{1-r} = \displaystyle \frac{a_1}{1-r}$

Formula for an infinite geometric series (Part 9)

I continue this series of posts by considering the formula for an infinite geometric series. Somewhat surprisingly (to students), the formula for an infinite geometric series is actually easier to remember than the formula for a finite geometric series.

One way of deriving the formula parallels yesterday’s post. If $a_1, a_2, a_3, \dots$ are the first terms of an infinite geometric sequence, let

$S = a_1 + a_2 + a_3 + \dots$

Recalling the formula for an geometric sequence, we know that

$a_2 = a_1 r$

$a_3 = a_1 r^2$

$\vdots$

Substituting, we find

$S = a_1 + a_1 r+ a_1 r^2 \dots$

For example, if $a_1 = \displaystyle \frac{1}{2}$ and $r = \displaystyle \frac{1}{2}$ , we have

$S = \displaystyle \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots$

This is perhaps the world’s most famous infinite series, as this is the subject of Zeno’s paradox. When I teach infinite series in class, I often engage the students by reminding students about Zeno’s paradox and then show them this clip from the 1994 movie I.Q.

This clip is almost always a big hit with my students.

Even after showing this clip, some students resist the idea that an infinite series can have a finite answer. For such students, I use a physical demonstration: I walk half-way across the classroom, then a quarter, and so on… until I walk head-first into a walk at full walking speed. The resulting loud thud usually confirms for students that an infinite sum can indeed have a finite answer.

P.S. PhD Comics recently had a cartoon concerning Zeno’s paradox. Source: http://www.phdcomics.com/comics/archive.php?comicid=1610

Here’s another one. Source: http://www.xkcd.com/994/

Formula for a finite geometric series (Part 8)

As I’ve said before, I’m not particularly a fan of memorizing formulas. Apparently, most college students aren’t fans either, because they often don’t have immediate recall of certain formulas from high school when they’re needed in the collegiate curriculum.

While I’m not a fan of making students memorize formulas, I am a fan of teaching students how to derive formulas. Speaking for myself, if I ever need to use a formula that I know exists but have long since forgotten, the ability to derive the formula allows me to get it again.

Which leads me to today’s post: the derivation of the formulas for the sum of a finite geometric series. This topic is commonly taught in Precalculus but, in my experience, is often forgotten by students years later when needed in later classes.

Like its counterpart for arithmetic series, the formula for a finite geometric series can be derived using the patented Bag of Tricks. Socrates gave the Bag of Tricks to Plato, Plato gave it to Aristotle, it passed down the generations, my teacher taught the Bag of Tricks to me, and I teach it to my students.

If $a_1, \dots, a_n$ are the first $n$ terms of an geometric sequence, let

$S = a_1 + a_2 + a_3 + \dots + a_{n-1} + a_n$

Recalling the formula for an geometric sequence, we know that

$a_2 = a_1 r$

$a_3 = a_1 r^2$

$\vdots$

$a_{n-1} = a_1 r^{n-2}$

$a_n = a_1 r^{n-1}$

Substituting, we find

$S = a_1 + a_1 r+ a_1 r^2 \dots + a_1 r^{n-2} + a_1 r^{n-1}$

At this point, we use something different from the patented Bag of Tricks: we multiply both sides by $-r$ .

$-rS = -a_1r - a_1 r^2- a_1 r^3 \dots - a_1 r^{n-1} - a_1 r^n$

Next, we add the two equations. Notice that almost everything cancels on the right-hand side. The $a_1 r$ cancel, the $a_1 r^2$ cancel, yada yada yada, and the $a_1 r^{n-1}$ cancel. The only terms that remain are $a_1$ and $-a_1 r^n$ . So

$S - rS = a_1 - a_1 r^n$

$S(1-r) = a_1 (1- r^n)$

$S = \displaystyle \frac{a_1 ( 1-r^n) }{1-r}$

A quick pedagogical note: I find that this derivation “sells” best to students when I multiply by $-r$ and add, as opposed to multiplying by $r$ and subtracting.

This formula is also a straightforward consequence of the factorization formula

$x^n - y^n = (x-y)(x^{n-1} + x^{n-2} y + \dots +x y^{n-2} + y^{n-1})$

Just let $x=1$ and $y=r$ , and then multiply both sides by the first term $a_1$ .

However, in my experience, most students don’t have instant recall of this formula either. They can certainly remember the formula for the difference of two squares (which is a special case of the above formula), but they often can’t remember that the difference of two cubes has a formula. (And, while I’m on the topic, they also can’t remember that the sum of two cubes can always be factored.)

Pedagogically, the most common mistake that I see students make when using this formula is using the wrong exponent on the right-hand side. For example, suppose the problem is to simplify

$48 +24+ 12 + 6 + 3 + 1.5 + 0.75 + 0.375$

Here’s the common mistake: student solve for $n$ using the formula for a geometric sequence. They solve for the unknown exponent (often using logarithms) and find that $0.375 = 48 (0.5)^7$ . They conclude that $n=7$ , and then plug into for formula for a geometric series:

$S = \displaystyle \frac{48 ( 1-(0.5)^7) }{1-0.5} = 95.25$ (incorrect)

This answer is clearly wrong, since the sum of the original series must have a $5$ in the thousandths place. The answer $95.25$ is the correct answer to the wrong question — that’s the sum of the first seven terms of the sequence (stopping at $0.75$ ), but the original series has eight terms. Using the formula correctly, we find

$S = \displaystyle \frac{48 ( 1-(0.5)^8) }{1-0.5} = 95.625$ (correct)

Not surprisingly, the difference between the incorrect and correct answers is $0.375$ , the eighth term.

To help students avoid this mistake, I re-emphasize that the number $n$ stands for the number of terms in the series. In particular, it does not mean the exponent needed to give the last term in the series. That exponent, of course, is $n-1$ , not $n$ .

Why does 0.999… = 1? (Part 1)

Our decimal number system is so wonderful that it’s often taken for granted. (If you doubt me, try multiplying $12$ and $61$ or finding an $18\%$ tip on a restaurant bill using only Roman numerals.)

However, there’s one little quirk about our numbering system that some students find quite unsettling:

If a number has a terminating decimal representation, then the same number also has a second different terminating decimal representation. (However, a number that does not have a terminating decimal representation does not have a second representation.)

Stated another way, a decimal representation corresponds to a unique real number. However, a real number may not have a unique decimal representation.

Some (perhaps many) students find such equalities to be unsettling at first glance, and for good reason. They’d prefer to think that there is a one-to-one correspondence to the set of real numbers and the set of decimal representations. Stated more simply, students are conditioned to think that if two number look different (like $24$ and $25$ ), then they ought to be different.

However, there’s a subtle difference between a number and a numerical representation. The number $1$ is defined to be the multiplicative identity in our system of arithmetic. However, this number has two different representations in our numbering system: $1$ and $0.999\dots$ . (Not to mention its representation in the numbering systems of the ancient Romans, Babylonians, Mayans, etc.)

As usual, let $[0,1]$ be the set of real numbers from $0$ to $1$ (inclusive), and let $D$ be the set of decimal representations of the form $0.d_1 d_2 d_3 \dots$ . Then there’s clearly a function $f : D \to \mathbb{R}$ , defined by

$f(0.d_1 d_2 d_3\dots) = \displaystyle \sum_{i=1}^\infty \frac{d_n}{10^n}$

If I want to give my students a headache, I’ll ask, “In Calculus II, you saw that some series converge and some series diverge. So what guarantee do we have that this series actually converges?” (The convergence of the right series can be verified using the Direct Comparsion Test, the fact that $d_i \le 9$ , and the formula for an infinite geometric series.)

In the language of mathematics: Using the completeness axiom, it can be proven (though no student psychologically doubts this) that $f$ maps $D$ onto $[0,1]$ . In other words, every decimal representation corresponds to a real number, and every real number has a decimal representation. However, the function $f$ is a surjection but not a bijection. In other words, a real number may have more than one decimal representation.

This is a big conceptual barrier for some students — even really bright students — to overcome. They’re not used to thinking that two different decimal expansions can actually represent the same number.

The two most commonly shown equal but different decimal representations are $0.999\dots = 1$ . Other examples are

$0.125 = 0.124999\dots$

$3.458 = 3.457999 \dots$

In this series, I will discuss some ways of convincing students that $0.999\dots = 1$ . That said, I have met a few math majors within a semester of graduating — that is, they weren’t dummies — who could recite all of these ways and were perhaps logically convinced but remained psychologically unconvinced. The idea that two different decimal representations could mean the same number just remained too high of a conceptual barrier for them to hurdle.

Method #1. This first technique is accessible to any algebra or pre-algebra student who’s comfortable assigning a variable to a number. We convert the decimal representation to a fraction using something out of the patented Bag of Tricks. If students aren’t comfortable with the first couple of steps (as in, “How would I have thought to do that myself?”), I tell my usual tongue-in-cheek story: Socrates gave the Bag of Tricks to Plato, Plato gave it to Aristotle, it passed down the generations, my teacher taught the Bag of Tricks to me, and I teach it to my students.

Let $x =0.999\dots$ . Multiply $x$ by $10$ , and subtract:

$10x = 9.999\dots$

$x = 0.999\dots$

$\therefore (10-1)x = 9$

$x =1$

$0.999\dots = 1$

Thoughts on 1/7 and other rational numbers (Part 4)

In Part 3 of this series, I considered the conversion of a repeating decimal expansion into a fraction. This was accomplished by an indirect technique which was pulled out of the patented Bag of Tricks. For example, if $x = 0.\overline{432} = 0.432432432\dots$ , we start by computing $1000x$ and then subtracting.

$1000x = 432.432432\dots$

$x = 0.432432\dots$

$999x = 432$

$x = \displaystyle \frac{432}{999} = \displaystyle \frac{16}{37}$

As mentioned in Part 3, most students are a little bit skeptical that this actually works, and often need to type the final fraction into a calculator to be reassured that the method actually works. Most students are also a little frustrated with this technique because it does come from the Bag of Tricks. After all, the first two steps (setting the decimal equal to $x$ and then multiplying $x$ by $1000$ ) are hardly the most intuitive things to do first… unless you’re clairvoyant and know what’s going to happen next.

In this post, I’d like to discuss a more direct way of converting a repeating decimal into a fraction. In my experience, this approach presents a different conceptual barrier to students. This is a more direct approach, and so students are more immediately willing to accept its validity. However, the technique uses the formula for an infinite geometric series, which (unfortunately) most senior math majors cannot instantly recall. They’ve surely seen the formula before, but they’ve probably forgotten it because a few years have passed since they’ve had to extensively use the formula.

Anyway, here’s the method applied to $0.\overline{432}$ . To begin, we recall the meaning of a decimal representation in the first place:

$0.432432432 \dots = \displaystyle \frac{4}{10} + \frac{3}{100} + \frac{2}{1000} + \displaystyle \frac{4}{10^4} + \frac{3}{10^5} + \frac{2}{10^6} + \displaystyle \frac{4}{10^7} + \frac{3}{10^8} + \frac{2}{10^9} + \dots$

Combining fractions three at a time (matching the length of the repeating block), we get

$0.432432432 \dots = \displaystyle \frac{432}{10^3} + \displaystyle \frac{432}{10^6} + \frac{432}{10^9} + \dots$

This is an infinite geometric series whose first term is $\displaystyle \frac{432}{10^3}$ , and the common ratio that’s multiplied to go from one term to the next is $\displaystyle \frac{1}{10^3}$ . Using the formula for an infinite geometric series and simplifying, we conclude

$0.432432432 \dots = \displaystyle \frac{ \quad \displaystyle \frac{432}{1000} \quad }{\quad 1 - \displaystyle \frac{1}{1000} \quad}$

$0.432432432 \dots = \displaystyle \frac{ \displaystyle \quad \frac{432}{1000} \quad}{ \displaystyle \quad \frac{999}{1000} \quad}$

$0.432432432 \dots = \displaystyle \frac{ 432}{ 999}$

$0.432432432 \dots = \displaystyle \frac{ 16}{ 37}$

For what it’s worth, the decimal representation could have been simplified by using three separate geometric series. Some students find this to be more intuitive, combining the unlike fractions at the final step as opposed to the initial step.

$0.432432432 \dots = \left( \displaystyle \frac{4}{10} + \frac{4}{10^4} + \displaystyle \frac{4}{10^7} + \dots \right)$

$\quad \quad \quad \quad + \left( \displaystyle \frac{3}{100} + \frac{3}{10^5} + \displaystyle \frac{3}{10^8} + \dots \right)$

$+ \left( \displaystyle \frac{2}{1000} + \frac{2}{10^6} + \displaystyle \frac{2}{10^9} + \dots \right)$

$0.432432432 \dots = \displaystyle \frac{ \quad \displaystyle \frac{4}{10} \quad }{\quad 1 - \displaystyle \frac{1}{1000} \quad} + \frac{ \quad \displaystyle \frac{3}{100} \quad }{\quad 1 - \displaystyle \frac{1}{1000} \quad} + \frac{ \quad \displaystyle \frac{2}{1000} \quad }{\quad 1 - \displaystyle \frac{1}{1000} \quad}$

$0.432432432 \dots = \displaystyle \frac{ \quad \displaystyle \frac{4}{10} \quad }{\quad \displaystyle \frac{999}{1000} \quad} + \frac{ \quad \displaystyle \frac{3}{100} \quad }{\quad \displaystyle \frac{999}{1000} \quad} + \frac{ \quad \displaystyle \frac{2}{1000} \quad }{\quad \displaystyle \frac{999}{1000} \quad}$

$0.432432432 \dots = \displaystyle \frac{ 400}{ 999} + \frac{30}{999} + \frac{2}{999}$

$0.432432432 \dots = \displaystyle \frac{ 432}{ 999}$

$0.432432432 \dots = \displaystyle \frac{ 16}{ 37}$

Finally, this direct technique also works for repeating decimals with a delay, like $0.41\overline{6}$ .

$0.41666\dots = \displaystyle \frac{4}{10} + \frac{1}{100} + \left( \frac{6}{1000} + \frac{6}{10^4} + \frac{6}{10^5} + \dots \right)$

$0.41666\dots = \displaystyle \frac{4}{10} + \frac{1}{100} + \displaystyle \frac{ \quad \displaystyle \frac{6}{1000} \quad }{\quad 1 - \displaystyle \frac{1}{10} \quad}$

$0.41666\dots = \displaystyle \frac{4}{10} + \frac{1}{100} +\displaystyle \frac{ \quad \displaystyle \frac{6}{1000} \quad }{\quad \displaystyle \frac{9}{10} \quad}$

$0.41666\dots = \displaystyle \frac{4}{10} + \frac{1}{100} +\frac{6}{900}$

$0.41666\dots = \displaystyle \frac{375}{900}$

$0.41666\dots = \displaystyle \frac{5}{12}$

Thoughts on 1/7 and other rational numbers (Part 3)

In Part 2 of this series, I discussed the process of converting a fraction into its decimal representation. In this post, I consider the reverse: starting with a decimal representation, and ending with a fraction.

Let me say at the onset that the process I’m about to describe appears to be a dying art. When I show this to my math majors who want to be high school teachers, roughly half have either not seen it before or else have no memory of seeing it before. (As always, I hold my students blameless for the things that they were simply not taught at a younger age, and part of my job is repairing these odd holes in their mathematical backgrounds so that they’ll have their best chance at becoming excellent high school math teachers.) I’m guessing that this algorithm is a dying art because of the ease and convenience of modern calculators.

So let me describe how I describe this procedure to my students. To begin, suppose that we’re given a repeating decimal like $0.\overline{432} = 0.432432432\dots$ . How do we change this into a decimal? Let’s call this number $x$ .

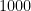I’m now about to do something that, if you don’t know what’s coming next, appears to make no sense. I’m going to multiply $x$ by $1000$ . Students often give skeptical, quizzical, and/or frustrated looks about this non-intuitive next step… they’re thinking, “How would I ever have thought to do that on my own?” To allay these concerns, I explain that this step comes from the patented Bag of Tricks. Socrates gave the Bag of Tricks to Plato, Plato gave it to Aristotle, it passed down the generations, my teacher taught the Bag of Tricks to me, and I teach it to my students. Multiplying by 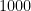$1000$ on the next step is absolutely not obvious, unless you happen to know via clairvoyance what’s going to come next.

Anyway, let’s write down $x$ and also $1000x$ .

$1000x = 432.432432\dots$

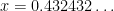
$x = 0.432432\dots$

Notice that the decimal parts of both $x$ and $1000x$ are the same. Subtracting, the decimal parts cancel, leaving

$999x = 432$

$x = \displaystyle \frac{432}{999} = \displaystyle \frac{16}{37}$

In my experience, most students — even senior math majors who have taken a few theorem-proof classes and hence are no dummies — are a little stunned when they see this procedure for the first time. To make this more real and believable to them, I then ask them to pop out their calculators to confirm that this actually worked. (Indeed, many students need this confirmation to be psychologically sure that it really did work.)

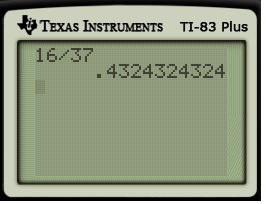
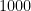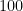Then I ask my students, why did we multiply by $1000$ ? They’ll usually give the correct answer: so that the decimal parts will cancel. My follow-up question is, what should we do if the decimal is $0.\overline{24}$ ? They’ll usually respond that we should multiply by $100$ or, in general, by $10^n$ , where $n$ is the length of the repeating block.

This strategy, of course, works for $0.\overline{142857}$, eventually yielding

$0.\overline{142587} = \displaystyle \frac{142857}{999999} = \displaystyle \frac{1}{7}$

after cancellation.

The same procedure works for decimal expansions with a delay, like $x = 0.72\overline{3}$ . This time, I’ll ask them how we should go about changing this into a fraction. I usually get at least one of three responses. I love getting multiple responses, as this gives the students a chance to came the “different” answers, compare the different strategies, and

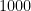Answer #1. Multiply $x$ by $1000$ since the repeating pattern starts at the 3rd decimal place.

$1000x = 723.333\dots$

$x = 0.7233\dots$

$\therefore 999x = 722.61$

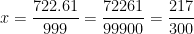
$x =\displaystyle\frac{722.61}{999} = \displaystyle\frac{72261}{99900} = \displaystyle \frac{217}{300}$

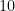Answer #2. Multiply $x$ by $10$ since the repeating block has length 1.

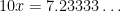
$10x = 7.23333\dots$

$x = 0.7233\dots$

$\therefore 9x = 6.51$

$x = \displaystyle \frac{6.51}{9} = \displaystyle\frac{651}{900} = \displaystyle\frac{217}{300}$

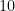Answer #3. First multiply $x$ by 100 to get rid of the delay. Then multiply $100 x$ by an extra $10$ since the repeating block has length 1.

$1000x = 723.333\dots$

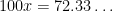
$100x = 72.33\dots$

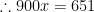
$\therefore 900x = 651$

$x = \displaystyle\frac{651}{900} = \displaystyle\frac{217}{300}$

The above discussion concerned repeating decimals. For completeness, converting terminating decimals into a fraction is easy. For example,

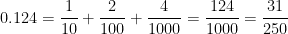
$0.124 = \displaystyle \frac{1}{10} + \frac{2}{100} + \frac{4}{1000} = \displaystyle \frac{124}{1000} = \displaystyle \frac{31}{250}$

One more thought. The concept behind Part 2 of this series shows that a rational number of the form $k/n$ , where both $k$ and $n$ are integers, must have either a terminating decimal expansion or else a repeating decimal expansion (possibly with a delay). In this post, we went the other direction. Therefore, we have the basis for the following theorem.

Theorem. A number $x$ is rational if and only if it has either a terminating decimal expansion or else a repeating decimal expansion.

The contrapositive of this theorem is perhaps intuitively obvious.

Theorem. A number $x$ is irrational if and only if it has a non-terminating and non-repeating decimal expansion.

In my experience, most students absolutely believe both of these theorems. For example, most students believe that $\sqrt{2}$ has a decimal expansion that neither terminates nor repeats. That said, most math majors are surprised to discover that it does take quite a bit of work — like a formal write-up of Parts 2 and 3 of this series — to actually prove this statement from middle-school mathematics.