Calculators and complex numbers (Part 3)

In this series of posts, I explore properties of complex numbers that explain some surprising answers to exponential and logarithmic problems using a calculator (see video at the bottom of this post). These posts form the basis for a sequence of lectures given to my future secondary teachers.

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

where $r = |z| = \sqrt{a^2 + b^2}$ and $\tan \theta = b/a$ , with $\theta$ in the appropriate quadrant. As noted before, this is analogous to converting from rectangular coordinates to polar coordinates.

There’s a shorthand notation for the right-hand side ( $r e^{i \theta}$ ) that I’ll justify later in this series.

Why is this important? When students first learn to multiply complex numbers like $1+i$ and $2+i$ , they are taught to just distribute (or, using the nomenclature that I don’t like, FOIL it out):

$(1+i)(1+2i) = 1 + 2i + i + 2i^2 = 1 + 3i - 2 = -1 + 3i$ .

The trigonometric form of a complex number permits a geometric interpretation of multiplication, given in the following theorem.

Theorem. $\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right] = r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

Proof. As above, we distribute (except for the $r_1$ and $r_2$ terms):

$\left[ r_1 (\cos \theta_1 + i \sin \theta_1) \right] \cdot \left[ r_2 (\cos \theta_2 + i \sin \theta_2) \right]$

$= r_1 r_2 (\cos \theta_1 \cos \theta_2 + i \cos \theta_1 \sin \theta_2 + i \sin \theta_1 \cos \theta_2 + i^2 \sin \theta_1 \sin \theta_2$

$= r_1 r_2 (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 + i[ \sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2])$

$= r_1 r_2 (\cos [\theta_1+\theta_2] + i \sin [\theta_1+\theta_2])$ .

When actually doing this in class, the big conceptual jump for students is the last step. So I make a big song-and-dance routine out of this:

Cosine of the first times cosine of the second minus sine of the first times sine of the second… where have I seen this before?

The idea is for my students to search deep into their mathematical memories until they recall the appropriate trig identity.

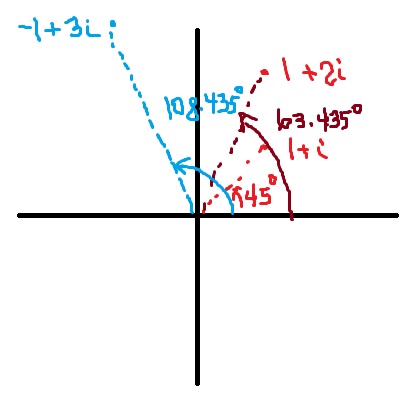
For the original multiplication problem, we see that

$1+i = \sqrt{2} \left( \cos 45^\circ + i \sin 45^\circ \right)$

$1 + 2i = \sqrt{5} \left( \cos[\tan^{-1} 2] + i \sin[\tan^{-1} 2] \right) \approx \sqrt{5} \left( \cos 63.435^\circ + i \sin 63.435^\circ \right)$

Therefore, the product of $1+i$ and $1+2i$ will be a distance of $\sqrt{2} \cdot \sqrt{5} = \sqrt{10}$ from the origin, and the angle from the positive real axis will be $45^\circ + \tan^{-1} 2 \approx 45^\circ + 63.435^\circ = 108.435^\circ$ . Indeed,

$-1 + 3i \approx \sqrt{10} \left( \cos 108.435^\circ + i \sin 108.435^\circ \right)$ .

green line

For completeness, here’s the movie that I use to engage my students when I begin this sequence of lectures.

Calculators and complex numbers (Part 2)

In yesterday’s post, I showed a movie (also provided at the bottom of this post) that calculators can return surprising answers to exponential and logarithmic problems involving complex numbers. In this series of posts, I hope to explain why the calculator returns these results.

To begin, we recall that the trigonometric form of a complex number $z = a+bi$ is

$z = r(\cos \theta + i \sin \theta)$

where $r = |z| = \sqrt{a^2 + b^2}$ and $\tan \theta = b/a$ , with $\theta$ in the appropriate quadrant.

For example, the point $z = -\sqrt{3} + i$ is in the second quadrant of the complex plane. The modulus is

$r = \sqrt{ (-\sqrt{3})^2 + (1)^2 } = \sqrt{4} = 2$ .

(Notice that $1$ , and not $i$ , appears in the above expression.) Also,

$\tan \theta = \displaystyle \frac{1}{-\sqrt{3}}$ , so that $\theta = \displaystyle -\frac{\pi}{6} + n \pi$

Since $-\sqrt{3} + i$ is in the second quadrant, we choose $\theta = \displaystyle -\frac{\pi}{6} + \pi = \displaystyle \frac{5\pi}{6}$ . Therefore,

$-\sqrt{3} + i = \displaystyle 2 \left( \cos \frac{5\pi}{6} + \sin \frac{5\pi}{6} \right)$

This can be checked by simply evaluating the right-hand side and distributing:

$\displaystyle 2 \left( \cos \frac{5\pi}{6} + \sin \frac{5\pi}{6} \right) = \displaystyle 2 \left( -\frac{\sqrt{3}}{2} + i \frac{1}{2} \right) = -\sqrt{3} +i$

When teaching this in class, I’ll run through about 2-4 more examples to make sure that this concept is stuck in my students’ heads.

Notes:

The angle $\theta$ is not uniquely defined… any angle that is coterminal with $\frac{5\pi}{6}$ would also have worked. For example,

$-\sqrt{3} + i = \displaystyle 2 \left( \cos \frac{17\pi}{6} + \sin \frac{17\pi}{6} \right)$

and

$-\sqrt{3} + i = \displaystyle 2 \left( \cos \frac{-7\pi}{6} + \sin \frac{-7\pi}{6} \right)$

It’s really important to remember that $\theta$ need not be equal to $\displaystyle \tan^{-1} \frac{b}{a}$ . After all, the arctangent of an angle must lie between $-\pi/2$ and $\pi/2$ , which won’t work for complex numbers in either the second or third quadrant. That said, it is true that

$-\sqrt{3} + i = \displaystyle -2 \left( \cos \frac{-\pi}{6} + \sin \frac{-\pi}{6} \right)$

The above procedure is also the essence of converting from rectangular coordinates to polar coordinates (or vice versa), which is a function pre-programmed on many scientific calculators.
When teaching this topic, I often use physical humor to get the above points across.

I’ll pick the direction parallel to the chalkboard to be the positive real axis, and the direction perpendicular to the chalkboard (i.e., pointing toward my students) as the positive imaginary axis. I’ll pick some convenient spot in front of the class to be the origin.
Standing at the origin, I’ll face the positive real axis, spin in an angle of $5\pi/6 = 150^\circ$ , and take two steps to arrive at the point $-\sqrt{3} + i$ .
Returning to the origin, I’ll face the positive real axis, spin the other direction in an angle of $-210^\circ$ , and take two steps to arrive at the same point.
Returning to the origin, I’ll face the positive real axis, spin in an angle of $510^\circ$ (getting more than a little dizzy while doing so), and take two steps to arrive at the same point.
Returning to the origin, I’ll face the positive real axis, spin in an angle of only $-30^\circ$ , and take two steps backwards (while doing the moonwalk) to arrive at the same point.

green line

We will need to use this concept of writing a complex number in trigonometric form in order to explain the calculator’s results. For completeness, here’s the movie that I used to begin this series of posts.

Calculators and complex numbers (Part 1)

What is $\ln(-5)$ ? Or $(-8)^{1/3}$ ? Easy, right? Well, let’s plug into a calculator and find out. (Click anywhere in the image below to start the movie. The important stuff is the screen at the top; you can see the keystrokes that I used if you following the mouse arrow toward the bottom.)

In this series of posts, I’ll try to explain why the calculator provides these unexpected answers. This series of posts will have 24 posts (!) and will contain some fairly sophisticated mathematics to explain why the calculator does what it does as well as some pedagogical discussion when I present these topics to my class of future secondary teachers. Each post can be thought of as a 5-10 minute portion of one of my lectures.

Prepare to Have Your Mind Blown by a Balloon and a Minivan

For more information, see http://io9.com/prepare-to-have-your-mind-blown-by-a-balloon-and-a-mini-1565303363?utm_campaign=socialflow_io9_facebook&utm_source=io9_facebook&utm_medium=socialflow

See also Smarter Every Day’s channel: http://www.youtube.com/user/destinws2

Neil Armstrong on Being a Nerd

Accommodating Blind Students Taking Mathematics

This was another interesting pedagogical article from the February/March 2014 issue of FOCUS, published by the Mathematical Association of America. I had never heard of the Nemeth code, the braille for mathematical notation.

http://digitaleditions.walsworthprintgroup.com/display_article.php?id=1639571

Flipping to Offer Low-Enrollment Courses

I just read a very interesting article about how an instructor at Ohio Dominican University is simultaneously teaching several upper-level mathematics courses with low enrollment by flipping the classroom (using the catchy title One-Room Schoolhouse). Here’s the article: http://digitaleditions.walsworthprintgroup.com/display_article.php?id=1639570

Approximating pi

I was recently interviewed by my city’s local newspaper about $\pi$ Day and the general fascination with memorizing the digits of $\pi$ . I was asked by the reporter if the only constraint in our knowledge of the digits of $\pi$ was the ability of computers to calculate the digits, and I answered in the affirmative.

Here’s the current state-of-the-art for calculating the digits of $\pi$ . Amazingly, this expression was discovered 1995… in other words, very recently.

$\pi = \displaystyle \sum_{n=0}^\infty \frac{1}{16^n} \left( \frac{4}{8n+1} - \frac{2}{8n+4} - \frac{1}{8n+5} - \frac{1}{8n+6} \right)$

Because of the term $16^n$ in the denominator, this infinite series converges very quickly.

Proof: If $k < 8$ , then we calculate the integral $I_k$ , defined below:

$I_k = \displaystyle \int_0^{1/\sqrt{2}} \frac{x^{k-1}}{1-x^8} dx$

$= \displaystyle \int_0^{1/\sqrt{2}} x^{k-1} \sum_{n=0}^\infty x^{8n} dx$

$= \displaystyle \int_0^{1/\sqrt{2}} \sum_{n=0}^\infty x^{8n+k-1} dx$

$= \displaystyle \sum_{n=0}^\infty \int_0^{1/\sqrt{2}} x^{8n+k-1} dx$

$= \displaystyle \sum_{n=0}^\infty \left[ \frac{x^{8n+k}}{8n+k} \right]^{1/\sqrt{2}}_0$

$= \displaystyle \sum_{n=0}^\infty \frac{1}{8n+k} \left[ \left( \frac{1}{\sqrt{2}} \right)^{8n+k} - 0 \right]$

$= \displaystyle \sum_{n=0}^\infty \frac{1}{2^{k/2}} \frac{1}{16^n (8n+k)}$

We now form the linear combination $P = 4\sqrt{2} I_1 - 8 I_4 - 4\sqrt{2} I_5 - 8 I_6$ :

$P = \displaystyle \sum_{n=0}^\infty \left( \frac{4\sqrt{2}}{2^{1/2}} \frac{1}{16^n (8n+1)} - \frac{8}{2^{4/2}} \frac{1}{16^n (8n+4)} - \frac{4\sqrt{2}}{2^{5/2}} \frac{1}{16^n (8n+5)} - \frac{8}{2^{6/2}} \frac{1}{16^n (8n+6)} \right)$

$P = \displaystyle \sum_{n=0}^\infty \frac{1}{16^n} \left( \frac{4}{8n+1} - \frac{2}{8n+4} - \frac{1}{8n+5} - \frac{1}{8n+6} \right)$

Also, from the original definition of the $I_k$ ,

$P = \displaystyle \int_0^{1/\sqrt{2}} \frac{4\sqrt{2} - 8x^3 -4\sqrt{2} x^4 - 8x^5}{1-x^8} dx$ .

Employ the substitution $x = y/\sqrt{2}$ :

$P = \displaystyle \int_ 0^1 \frac{4\sqrt {2} - 2\sqrt {2} y^3 - \sqrt {2} y^4 - \sqrt {2} y^5}{1 - y^8/16}\frac {dy} {\sqrt {2}}$

$P = \displaystyle \int_ 0^1 \frac{16 (4 - 2 y^3 - y^4 - y^5)}{16 - y^8} dy$

$P = \displaystyle \int_0^1 \frac{16(y-1)(y^2+2)(y^2+2y+2)}{(y^2-2)(y^2+2)(y^2+2y+2)(y^2-2y+2)} dy$

$P = \displaystyle \int_0^1 \frac{16y-16}{(y^2-2)(y^2-2y+2)} dy$

Using partial fractions, we find

$P = \displaystyle \int_ 0^1\frac{4 y}{y^2 - 2} dy - \int_ 0^1 \frac{4 y - 8}{y^2 - 2 y + 2} dy$

The expression on the right-hand side can be simplified using standard techniques from Calculus II and is equal to $\pi$ .

So that’s the proof… totally accessible to a student who has mastered concepts in Calculus II. But this begs the question: how in the world did anyone come up with the idea of starting with the integrals $I_k$ to develop an infinite series that leads to $\pi$ ? Let me quote from page 118 of J. Arndt and C. Haenel, $\pi -$ Unleashed (Springer, New York, 2000):

Certainly not by chance, even if luck played some part in the discovery. All three parties [David Bailey, Peter Borwein and Simon Plouffe] are established mathematicians who have been working with the number $\pi$ for a considerable time… Yet the series was not discovered through mathematical deduction or inference. Instead, the researchers used a tool called Computer Algebra System and a particular procedure called the “PSQL algorithm” to generate their series. They themselves write that they found their formula “through a combination of inspired testing and extensive searching.”

The original paper that announced the discovery of this series can be found at http://www.cecm.sfu.ca/personal/pborwein/PAPERS/P123.pdf.

MyScript MathPad: Handwriting LaTeX generator

LaTeX offers a free way for typing mathematical equations (for example, all of the mathematical equations on this website are written in LaTeX). Here’s an app for iPhones and iPads that I just found that says it can convert hand-written equations into LaTeX: https://itunes.apple.com/us/app/myscript-mathpad-handwriting/id674996719?mt=8

The Law of Averages

Colloquially, the Law of Averages dictates that what ought to happen does happen if it happens long enough. If a gambler plays a casino for a very long time, he is almost certainly guaranteed to lose. If a weak sports team plays a stronger team in a multiple-game series, then it is almost certain to lose the series.

However, if the gambler plays in the casino for only a little while, then there is a realistic (though less than 50%) chance of coming out ahead. And a weak sports team may defeat a stronger one if only one game is played… hence the appeal of the NCAA basketball tournament and, on a larger scale, the knockout stages of the World Cup.

In my statistics class, I use a simple simple spreadsheet to illustrate that $\hbox{SD}(K) = \sqrt{n p(1-p})$ for a sample count, but $\hbox{SD}(\hat{p}) = \displaystyle \sqrt{ \frac{p(1-p)}{n} }$ for a sample proportion. Here is one image from the spreadsheet:

The user can change the bright green cell to be any positive integer up to 5000. This number represents the number of simulated coins that are flipped. In the above example, ten coins are flipped. Column B shows the results of the simulated coins, while column C shows a running count of the number of heads that have appeared. In the above example, 7 of the 10 flips are heads, for an observed error of +2 (two more heads than the expected number of 5) and a percentage error of 20%.

In class, I would run the spreadsheet several times, and students will see that the observed error usually is in the range of -2 to +2, and the percentage error is usually in the range of -20% to +20%.

By contrast, look what happens when the number of flips increases to a large number, like 5000.

There is now a larger absolute error — in this case, -28. Of course, an absolute error of that size is impossible with 10 coin flips or even 50 coin flips. However, at the same time, the percentage error is now significantly smaller (only -0.56%).

This example gives evidence for the counter-intuitive result that the absolute error grows like $\sqrt{n}$ while the relative error decreases like $\sqrt{n}$ .