Engaging students: Fractions, decimals, and percents

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Belle Duran. Her topic, from Pre-Algebra: fractions, decimals, and percents.

D1. What interesting things can you say about the people who contributed to the discovery and/or development of this topic?

In the early 17^th century, calculating left all remainders in fraction form since the decimal has not been invented yet; this left a lot of redundant calculating for early mathematicians as well as a lot of room for small errors. Napier thought this to be “troublesome to mathematical practice” that he created an early version of a calculator known as Napier’s logarithms (an early appearance of the notorious laziness of mathematicians). They made computing numbers so simple that they became standard for astronomers, mathematicians, and anyone who did extensive computation; except for, of course, the people who had to construct the tables (consisting of over 30,000 numbers). Since it required a lot of computation, Napier resorted to expressing the logarithms in decimals. While Napier did not invent the decimal, he was considered one of the earliest to adopt and promote its use.

In 31 BC, ruler of Rome, August, taxed the sales of goods and slaves that were based on fractions of a hundred; trading usually involved large amounts of money that 100 became a common base for mathematical operations (“per cento” is Italian for “of hundred”). From the term, abbreviations were created such as “p 100 oder p cento”. In 1425, an uneducated scribe wrote “pc” and adorned the c with a little loop; from there, the sign evolved to a combination of loop and fraction bar.

D5. How have different cultures throughout time used this topic in their society?

Dating back to around 1650 B.C., Egyptian mathematicians used unit fractions; they would write five sevenths as 5/7= ½ + 1/7 + 1/14. Also, they did not use the same fraction twice, so they could not write 2/7 as 1/7+1/7, but 2/7=1/4+1/28.

In the Middle Ages, a bar over the units digit was used to separate a whole number from its fractional part, the idea deriving from Indian mathematics. It remains in common use as an under bar to superscript digits, such as monetary values.

A2. How could you as a teacher create an activity or project that involves your topic?

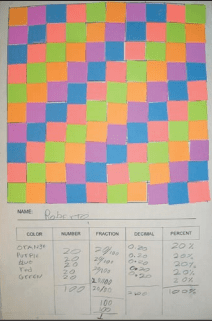
One way I, as a teacher, can create an activity that involves decimals, fractions and percents is to incorporate it with art. I found inspiration from an article titled, “Masterpieces to Mathematics: Using Art to Teach Fraction, Decimal, and Percent Equivalents.” Each student would receive a 100 square grid and a large amount of colored squares (red, green, blue, purple, orange) to create and glue on their square grid paper in a design of their choosing:

As seen on the image above, when the students were done with their masterpiece, they would have another sheet consisting of columns: color, number, fraction, decimal, and percent. They would list the colors they used under the color column, and then count the amount of squares of each color and record it in the number column. They would then convert the number of each color used compared to the total amount of squares (100) to a fraction, decimal, and percent. To further their understanding, I could ask the students to block out the outer squares and ask to calculate the new number of each color, fraction, decimal, and percent from the new total (64).

References: http://www.17centurymaths.com/contents/napier/jimsnewstuff/Napiers%20Bones/NapiersBones.html

http://www.decodeunicode.org/u+0025

< http://mason.gmu.edu/~jsuh4/math%20masterpiece.pdf>

< http://english.stackexchange.com/questions/177757/why-are-decimals-read-as-fractions-by-some-cultures>

< http://www.princeton.edu/~achaney/tmve/wiki100k/docs/Decimal_separator.html>

Did chaos cause mayhem in Jurassic Park?

I’ll happily link to this very readable introduction to chaos theory and the butterfly effect: http://plus.maths.org/content/did-chaos-cause-mayhem-jurassic-park

A sampling:

Suppose that we want to predict the future state of a system — the weather, for example — that is sensitive to initial conditions. We could measure its current state, and then iterate the system’s governing function on that seed value. This would yield an answer, but if our measurement of the system’s current state had been slightly imprecise, then the true result after a few iterations might be wildly different. Since empirical measurement with one hundred percent precision is not possible, this makes the predictive power of the model more than a few time-steps into the future essentially worthless.

The popular buzz-word for this phenonemon is the butterfly effect, a phrase inspired by a 1972 paper by the chaos theory pioneer Edward Lorenz. The astounding thing is that the unpredictability arises from a deterministic system: the function that describes the system tells you exactly what its next value will be. Nothing is left to randomness or chance, and yet accurate prediction is still impossible. To describe this strange state of affairs, Lorenz reportedly used the slogan

Chaos: When the present determines the future, but the approximate present does not determine the approximate future.

Chaotic dynamics have been observed in a wide range of phenomena, from the motion of fluids to insect populations and even the paths of planets in our solar system.

Improvisation in the Mathematics Classroom

This article discusses ways in which improvisational comedy games and exercises can be used in college mathematics classrooms to obtain a democratic and supportive environment for students. Using improv can help students learn to think creatively, take risks, support classmates, and solve problems. Both theoretical and practical applications are presented.

The full article can be found here: http://dx.doi.org/10.1080/10511970.2012.754809

Full reference: Andrea Young (2013) Improvisation in the Mathematics Classroom, PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 23:5, 467-476, DOI: 10.1080/10511970.2012.754809

What to Expect When You’re Expecting to Win the Lottery

I can’t think of a better way to tease this video than its YouTube description:

Recounting one of the stories included in his book How Not to Be Wrong: The Power of Mathematical Thinking, Jordan Ellenberg (University of Wisconsin-Madison) tells how a group of MIT students exploited a loophole in the Massachusetts State Lottery to win game after game, eventually pocketing more than $3 million.

A personal note: though I haven’t talked with him in years, Dr. Ellenberg and I were actually in the same calculus class about 30 years ago.

Engaging students: Graphing the sine and cosine functions

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Jessica Trevizo. Her topic, from Precalculus: graphing the sine and cosine functions.

How could you as a teacher create an activity or project that involves your topic?

For this activity students can either work with a partner or work individually. I enjoyed this activity because students are able to derive the sine and cosine functions on their own using fun materials other than the original paper and pencil. The knowledge that students should gain from this activity is the relationship between the unit circle and the sine/cosine function. Along with this activity, students will be practicing previous concepts learned such as converting degrees to radians, finding the domain/rage, and finding the x-intercepts and y-intercepts. Also, amplitude, period, and wavelength are important vocabulary words that can be introduced and applied to the parent functions. To complete the activity assign the students to write a paragraph comparing and contrasting both functions. In their paragraph make sure students include a discussion of the intercepts, maxima, minimum, and period. It is essential for the students to know how to graph the parent functions of sine and cosine and where they come from before teaching the students about the transformations of the functions.

http://illuminations.nctm.org/Lesson.aspx?id=2870

A.1 What interesting word problems using this topic can your students do now?

Real life word problems that involve the sine and cosine function can be used to keep the students engaged in the topic. Both of the functions can used to model situations that occur in real life in a daily basis such as; recording the path of the electric currents, musical tones, radio waves, tides, and weather patterns. Here is an example of a word problem, “Throughout the day, the depth of the water at the end of a dock in Bar Harbor, Maine varies with tides. The table shows the depths (in feet) at various times during the morning.” With the data provided the students are able to do several things such as: be able to use a trigonometric function to model the data and find the depth of the water at any specific time. Also, if a boat needs at least 10 feet of water to moor at the dock, the students should be able to figure out safe dock times for the boat.

How can technology be used to effectively engage students with this topic?

Most of the students are familiar with sound waves. As an engage go to www.onlinemictest.com and have the students observe the sound waves that appear on the screen as you speak. Many students will recognize the various sine and cosine functions on the screen. With the online mic test students are also able to make relationships between the sound and the wave. Download several different tones and play them so the sound waves of the tones appear on the screen. Have the students sketch the graph of a soft high note, soft low note, loud high note, and a loud low note. The following graphs should look similar to the figure below. Once all of the students have recorded their own observations have the students work with a partner to compare their graphs. Also give the students a minute or two so they can compare and contrast the 4 different graphs by using the new vocabulary that they learned such as amplitude and period. Students are able to remember the new vocabulary when they have opportunities to have discussions that require them to use them.

Engaging students: Compound interest

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Daniel Littleton. His topic, from Precalculus: compound interest.

How has this topic appeared in the news?

In a publication entitled Business Insider, Sam Ro published an article entitled “Every 25 Year Old In America Should See This Chart” on March 21, 2014. In this article Ro stated that in past times companies would offer pension plans to long term employees in order to support them in retirement. He goes on to state that in modern times employees need to contribute to retirement plans such as a 401K or an IRA in order to save for retirement. These plans function by the mathematical principle of compound interest. While the mechanics of compound interest are not presented in the article an illustration is shown how individuals who save their money through this formula accumulate a greater amount of money over time. He even presents a situation in which one individual can save money for a less amount of time than another and still accrue a greater total amount of savings because of compound interest. This illustration, presented below, can be a useful tool in engaging students in the possibilities that compound interest could have in their own futures.

This information was collected from the following web page on Friday, April 04, 2014; http://www.businessinsider.com/compound-interest-retirement-funds-2014-3.

How can this topic be used in your students’ future courses in mathematics or science?

Compound interest is introduced at the Pre-Calculus level of secondary education. At the Post-Secondary Education level compound interest is a concept that is included in several areas of study. For example, students that wish to study business will need to have a mastery of compound interest. Additionally, those studying finance or economics will constantly use the principle of compound interest in their computations. Not only does this formula come into play in the mathematics of monetary systems, but also in the workings of political science as well. Those that wish to pursue political aspirations will need a firm understanding of economics and the means by which funds can be grown over time. As is evident, compound interest is a mathematical formula, but like many realms of mathematics it affects multiple realms of interest and practice in a real world environment.

What interesting word problems using this topic can your students do now?

There are an innumerable amount of problems that can be presented to students involving compound interest. One could deal with the monetary worth of valuable or precious items. For instance, “A necklace is appraised at $7200. If the value of the necklace has increased at an annual rate of 7.2%, how much was it worth 15 years ago?” This question is asking the student to solve for the original principle of the necklace, rather than the accrued value which is given. Another problem could be “A sum of $7000 is invested at an interest rate of 7% per year. Find the time required for the money to double if the interest is compounded quarterly.” This problem requires the student to determine the amount of time necessary for the investment to yield the desired amount. These are only two problems that I have presented that will allow the students to practice the concept of compound interest. There are undoubtedly multiple others that could be written with the same effect.

An Evaluative Calculus Project: Applying Bloom’s Taxonomy to the Calculus Classroom

Every so often, I’ll publicize through this blog an interesting article that I’ve found in the mathematics or mathematics education literature that can be freely distributed to the general public. Today, I’d like to highlight Gizem Karaali (2011) An Evaluative Calculus Project: Applying Bloom’s Taxonomy to the Calculus Classroom, PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 21:8, 719-731, DOI: 10.1080/10511971003663971

Here’s the abstract:

In education theory, Bloom’s taxonomy is a well-known paradigm to describe domains of learning and levels of competency. In this article I propose a calculus capstone project that is meant to utilize the sixth and arguably the highest level in the cognitive domain, according to Bloom et al.: evaluation. Although one may assume that mathematics is a value-free discipline, and thus the mathematics classroom should be exempt from focusing on the evaluative aspect of higher-level cognitive processing, I surmise that we as mathematics instructors should consider incorporating such components into our courses. The article also includes a brief summary of my observations and a discussion of my experience during the Fall 2008 semester, when I used the project described here in my Calculus I course.

The full article can be found here: http://dx.doi.org/10.1080/10511971003663971

Hands on SET

Every so often, I’ll publicize through this blog an interesting article that I’ve found in the mathematics or mathematics education literature that can be freely distributed to the general public. Today, I’d like to highlight “Hands-on SET®,” by Hannah Gordon, Rebecca Gordon, and Elizabeth McMahon. Here’s the abstract:

SET^® is a fun, fast-paced game that contains a surprising amount of mathematics. We will look in particular at hands-on activities in combinatorics and probability, finite geometry, and linear algebra for students at various levels. We also include a fun extension to the game that illustrates some of the power of thinking mathematically about the game.

The full article can be found here: http://dx.doi.org/10.1080/10511970.2013.764368

Full reference: Hannah Gordon, Rebecca Gordon & Elizabeth McMahon (2013) Hands-on SET®, PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 23:7, 646-658, DOI: 10.1080/10511970.2013.764368

Creating a Culture of Inquiry in Mathematics Programs

Every so often, I’ll publicize through this blog an interesting article that I’ve found in the mathematics or mathematics education literature that can be freely distributed to the general public. Today, I’d like to highlight “Creating a Culture of Inquiry in Mathematics Programs,” by Jill Dietz. Here’s the abstract:

We argue that student research skills in mathematics should be honed throughout the curriculum just as such skills are built over time in the natural and physical sciences. Examples used in the mathematics program at St. Olaf College are given.

The full article can be found here: http://dx.doi.org/10.1080/10511970.2012.711804

Full reference:Jill Dietz (2013) Creating a Culture of Inquiry in Mathematics Programs, PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 23:9, 837-859, DOI: 10.1080/10511970.2012.711804

Engaging students: Synthetic Division

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission comes from my former student Chelsea Hancock. Her topic, from Precalculus: synthetic division.

The method of synthetic division is an alternative version of long division concerning polynomials. Synthetic division uses the basic mathematical skills of addition, subtraction, multiplication, and negative signs. They must also understand the definitions of polynomial, coefficient, and remainder. A polynomial is an expression with multiple terms, poly meaning “many” and nomial meaning “term.” A coefficient is a number used to multiply a variable. The remainder is the amount left over after division. Synthetic division involves multiplying, then adding or subtracting the coefficients of two polynomials. On some occasions, there will be a remainder after dividing the polynomials.

Mathematicians are lazy. That is a fact of life. One mathematician understood this, so in 1809 he created a cleaner, faster, and much simpler method for division. His name was Paolo Ruffini. In order to more efficiently divide polynomials, Ruffini invented the Ruffini’s Rule, known more commonly as synthetic division in today’s society. In 1783, he entered the University of Modena and he studied mathematics, medicine, philosophy and literature. Then, in 1798 he began teaching mathematics at the University of Modena. He was required to swear an oath of allegiance to the republic, but due to religious purposes, refused to do so. This resulted in the loss of his professorship and was prevented from teaching.

There are several videos on the Internet involving synthetic division, but there are two in particular that I personally think are excellent demonstrations of both the method itself and why it works. I have labeled these clips Video 1 and Video 2. Video 1 is a demonstration of the method in action, using a specific example involving numbers, walking the viewers through the process through the whole video. Video 2 explains why using synthetic division instead of using long division is the more efficient and less complicated method for dividing polynomials. The clip uses the same example used in Video 1, but this time the polynomials are divided using long division, walking the viewers through the process the entire time. As the narrator moves through the process, he makes connections between the synthetic division method and the long division method and draws conclusions between the two. By the end of the video, it is evident which is the cleanest method to use when concerning the division of polynomials. These videos not only give great tutorials on both methods of division, but allows the viewers to see the benefits and uses of synthetic division when it is possible to use it.

Video 1: