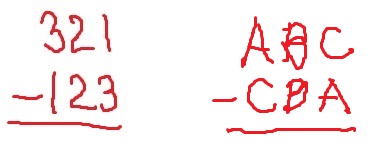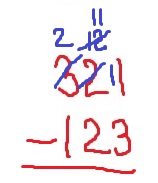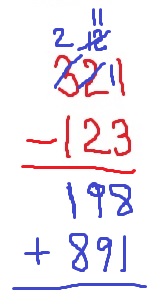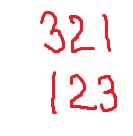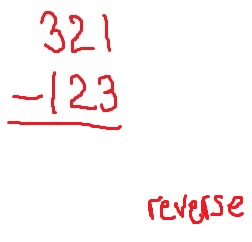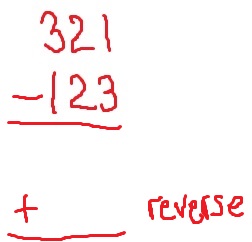My Mathematical Magic Show: Part 2c

Last March, on Pi Day (March 14, 2015), I put together a mathematical magic show for the Pi Day festivities at our local library, compiling various tricks that I teach to our future secondary teachers. I was expecting an audience of junior-high and high school students but ended up with an audience of elementary school students (and their parents). Still, I thought that this might be of general interest, and so I’ll present these tricks as well as the explanations for these tricks in this series. From start to finish, this mathematical magic show took me about 50-55 minutes to complete. None of the tricks in this routine are original to me; I learned each of these tricks from somebody else.

For my first trick, I chose the most boring of the routine. Everyone in the audience had a piece of paper and many had calculators. Here is the patter for the first trick:

To begin this trick, write down any three-digit number on your piece of paper. Just make sure that the first digit and the last digit are different.

(pause)

Now, reverse the digits and write down a new number. For example, if your number was 321, the new number will be 123.

(pause)

Now, subtract the small number from the big number. If your second number is larger, then put that number on top so that you can subtract the two numbers.

(pause)

Your difference is probably a three-digit number. However, if you ended up with a two-digit number, you can make it a three-digit number by putting a 0 in the hundreds place.

Next, I want you to reverse the digits of the difference to make a new three-digit number. Write this new number under the difference.

(pause)

Finally, add the last two three-digit numbers that you wrote down.

If everyone follows the instructions and does the arithmetic correctly, everyone will get a final answer of 1,089.

The next part of my mathematical magic show is showing everyone why the trick works. Yesterday, I gave an explanation suitable for upper elementary students. Today, I’ll give a more abstract explanation using algebra.

The succinct explanation can be found on Wikipedia:

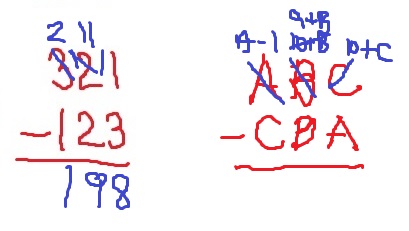
The spectator’s 3-digit number can be written as 100 × A + 10 × B + 1 × C, and its reversal as 100 × C + 10 × B + 1 × A, where 1 ≤ A ≤ 9, 0 ≤ B ≤ 9 and 1 ≤ C ≤ 9. (For convenience, we assume A > C; if A < C, we first swap A and C.) Their difference is 99 × (A − C). Note that if A − C is 0 or 1, the difference is 0 or 99, respectively, and we do not get a 3-digit number for the next step.

99 × (A − C) can also be written as 99 × [(A − C) − 1] + 99 = 100 × [(A − C) − 1] − 1 × [(A − C) − 1] + 90 + 9 = 100 × [(A − C) − 1] + 90 + 9 − (A − C) + 1 = 100 × [(A − C) − 1] + 10 × 9 + 1 × [10 − (A − C)]. (The first digit is (A − C) − 1, the second is 9 and the third is 10 − (A − C). As 2 ≤ A − C ≤ 9, both the first and third digits are guaranteed to be single digits.)

Its reversal is 100 × [10 − (A − C)] + 10 × 9 + 1 × [(A − C) − 1]. The sum is thus 101 × [(A − C) − 1] + 20 × 9 + 101 × [10 − (A − C)] = 101 × [(A − C) − 1 + 10 − (A − C)] + 20 × 9 = 101 × [−1 + 10] + 180 = 1089.

However, I don’t particularly care for the succinct explanation, and so I’d prefer to give my audience the following explanation. Let’s write our original three-digit number as $ABC$ , which of course stands for $100 \times A + 10 \times B + C$ . Then, when I reverse the digits, the new three-digit number will be $CBA$ , or $100 \times C + 10 \times B + A$ .

Of course, because the first number is bigger than the second number, this means that the first hundreds digit is bigger than the second hundreds digit. This means that the first ones digit has to be less than the second ones digit. In other words, when we subtract, we have to borrow from the tens place. However, the tens digits are the same for both numbers. That means that I have to borrow from the hundreds place also.

I’ll illustrate this for both subtraction problems:

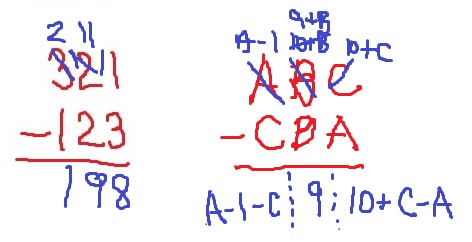
Now I’ll subtract. The hundreds digit will be $A - 1 - C$ . The tens digit will be $9 + B - B$ , or simply $9$ . Finally, the ones digit will be $10 + C - A$ . This is a little hard to write on a board, so I’ll add some dotted lines to separate the hundreds digits from the tens digit from the ones digit:

The next step is to reverse the digits and add:

I’ll begin with the ones digit:

$(10 + C - A) + (A - 1 - C) = 10 - 1 = 9$ .

No matter what, the ones digit is a 9.

Continuing with the tens digits, I get $9 + 9 = 18$ . I’ll write down $8$ and carry the $1$ to the next column.

Finally, adding the hundreds digits (and the extra $1$ ), I get

$1 + (A - 1 + C) + (10 + C - A) = 1 - 1 + 10$ .

Therefore, no matter the values of $A$ , $B$ , and $C$ , the end result must be $1089$ .

To complete the routine, I’ll ask a volunteer (usually a young child) to play the magician and repeat the trick for the audience. I consider this an important pedagogical step — the child enjoys being the magician on stage, while the audience lets the routine sink in one more time before I move on to the next magic trick.

My Mathematical Magic Show: Part 2b

For my first trick, I chose the most boring of the routine. Everyone in the audience had a piece of paper and many had calculators. Here is the patter for the first trick:

To begin this trick, write down any three-digit number on your piece of paper. Just make sure that the first digit and the last digit are different.

(pause)

Now, reverse the digits and write down a new number. For example, if your number was 321, the new number will be 123.

(pause)

Now, subtract the small number from the big number. If your second number is larger, then put that number on top so that you can subtract the two numbers.

(pause)

Your difference is probably a three-digit number. However, if you ended up with a two-digit number, you can make it a three-digit number by putting a 0 in the hundreds place.

Next, I want you to reverse the digits of the difference to make a new three-digit number. Write this new number under the difference.

(pause)

Finally, add the last two three-digit numbers that you wrote down.

If everyone follows the instructions and does the arithmetic correctly, everyone will get a final answer of 1,089.

The next part of my mathematical magic show is showing everyone why the trick works. The explanation depends on the mathematical sophistication of the audience. Today, I’ll give an explanation suitable for upper elementary students. Tomorrow, I’ll give a different explanation using algebra.

For today’s explanation, I’ll give an example:

However, the tens digits are the same for both numbers. That means that I have to borrow from the hundreds place also.

So, when I subtract, I’m guaranteed that the middle number will be a $9$ . Also, I’m guaranteed that the hundreds digit and the ones digit will add up to $9$ . In this example, the sum of the hundreds digits and the ones digits is equal to

$2 - 1 + 11 - 3$ .

We know that $11-1$ is equal to $10$ , and adding $2$ and subtracting $3$ is like subtracting $1$ . Therefore, the sum of the hundreds digit and the ones digit must be equal to $9$ .

The next step was reversing the digits of the difference:

Finally, I asked you to add these last two numbers. Remember, I had rigged things so that the hundreds and ones digits add up to $9$ . So the last digit of the sum must be $9$ . Also, I rigged things so that the tens digit must be $9$ . So, when I add, I get a sum of $18$ , and I leave the $8$ and carry the $1$ . Finally, the hundreds and ones digits add up to $9$ again. Adding the extra $1$ , I write down a sum of $10$ .

In tomorrow’s post, I’ll explain how the trick works using algebra.

My Mathematical Magic Show: Part 2a

For my first trick, I chose the most boring of the routine. Everyone in the audience had a piece of paper and many had calculators. I also had a small white board to write on at the front of the room. I began,

To begin this trick, write down any three-digit number on your piece of paper. Just make sure that the first digit and the last digit are different.

After waiting 10 seconds, I then said,

Now, reverse the digits and write down a new number. For example, if your number was 321, the new number will be 123.

And, to be sure my instructions are clear, I’ll write these numbers on my white board:

Next, I’ll say:

Now, subtract the small number from the big number. If your second number is larger, then put that number on top so that you can subtract the two numbers.

After waiting a minute or so, I’ll say,

Your difference is probably a three-digit number. However, if you ended up with a two-digit number, you can make it a three-digit number by putting a 0 in the hundreds place.

Next, I want you to reverse the digits of the difference to make a new three-digit number. Write this new number under the difference.

After everyone’s done, I’ll give my final instruction:

Finally, add the last two three-digit numbers that you wrote down.

After everyone’s done, I’ll point to someone and say, “Your final number was 1,089.” If he followed my instructions and did the arithmetic correctly, he’ll say, “You’re right.” Then I’ll point to someone else and say, “You also got 1,089.” She’ll also say, :”You’re right.” Then I’ll say, “Everyone got 1,089, right?”

Another (and more dramatic) way to end the routine is to hand a book of mine to someone, with the following instructions:

Your last number should have four digits. Cross out the last digit; you now will have a number with only three digits. Turn to that page number in this book. Then find the word on that page corresponding to the number you crossed out. For example, if you crossed out a one, point to the first word on the page. If you crossed out a two, point to the second word on the page. And so on.

Got it? The word you’re pointing to is XXXXXX.

And of course, I’ll get this right because, before starting the routine, I had already memorized the ninth word on page 108 of my book (the XXXXXX above). This looks really dramatic because it looks essentially random to the audience.

In tomorrow’s post, I’ll explain how the trick works.

My Mathematical Magic Show: Part 1

Last March, on Pi Day (March 14, 2015), I put together a mathematical magic show for the Pi Day festivities at our local library, compiling various tricks that I teach to our future secondary teachers. I thought that this might be of general interest, and so I’ll present these tricks as well as the explanations for these tricks in this series.

Before showing my own tricks, however, I have to pay homage to Arthur Benjamin, who is a Professor of Mathematics at Harvey Mudd College who’s also made a second career doing mathematical magic shows. See his Amazon page for the books that he’s published and his webpage at Harvey Mudd.

Collaborative Mathematics: Challenge 16

My colleague Jason Ermer at Collaborative Mathematics is back from summer hiatus and has published Challenge 16 on his website: http://www.collaborativemathematics.org/challenge16.html

Binary exercise

A wonderful application of binary arithmetic is the extra sense of accomplishment I enjoy after completing my daily regiment of 1000 push-ups and 1000 sit-ups.

Collaborative Mathematics: Challenge 14

I’m a few months late with this, but my colleague Jason Ermer at Collaborative Mathematics has published Challenge 14 on his website: http://www.collaborativemathematics.org/

Collaborative Mathematics: Challenge 13

I’m a few months late with this, but my colleague Jason Ermer at Collaborative Mathematics has published Challenge 13 on his website: http://www.collaborativemathematics.org/

Texans QB Ryan Fitzpatrick’s Son Shows Off Math Skills During Postgame Press Conference (Part 2)

From Bleacher Report:

Houston Texans quarterback Ryan Fitzpatrick… threw for 358 yards and six touchdowns in a 45-21 victory over the Tennessee Titans on Sunday [November 30, 2014]. However, [his son] Brady was the star of the postgame press conference.

Fitzpatrick put his son on the spot at the end of the press conference. In a matter of seconds, Brady was able to multiply 93 by 97 in his head.

Source: http://bleacherreport.com/articles/2284833-texans-qb-ryan-fitzpatricks-son-shows-off-math-skills-during-postgame-presser

After the thought bubble, I’ll reveal the likely way that young Brady did this.

Here’s a trick for multiplying two numbers in their 90s which is accessible to bright elementary-school students. We begin by multiplying out $(100-x)(100-y)$ :

$(100-x)(100-y) = 10,000 - 100x - 100y + xy$

$(100-100y) = 100(100 - [x+y]) + xy$

For $93 \times 97$ , we have $x = 7$ and $y = 3$ . So $x+y = 10$ , and $100 - [x+y] = 90$ . So the first two digits of the product is $90$ .

Also, $xy = 21$ . So the last two digits are $21$ .

Put them together, and we get the product $100 \times 90 + 21 = 9021$.

I don’t expect that young Brady knew all of this algebra, but I expect that he did the above mental arithmetic to put together the product. Well done, young man.

Texans QB Ryan Fitzpatrick’s Son Shows Off Math Skills During Postgame Press Conference (Part 1)

From Bleacher Report:

Houston Texans quarterback Ryan Fitzpatrick… threw for 358 yards and six touchdowns in a 45-21 victory over the Tennessee Titans on Sunday [November 30, 2014]. However, [his son] Brady was the star of the postgame press conference.

Fitzpatrick put his son on the spot at the end of the press conference. In a matter of seconds, Brady was able to multiply 93 by 97 in his head.

Source: http://bleacherreport.com/articles/2284833-texans-qb-ryan-fitzpatricks-son-shows-off-math-skills-during-postgame-presser

I’ll reveal the (likely) way that young Brady Fitzpatrick pulled this off tomorrow. In the meantime, I’ll leave a thought bubble if you’d like to try to figure it out on your own.