Solving Problems Submitted to MAA Journals (Part 4)

The following problem appeared in Volume 96, Issue 3 (2023) of Mathematics Magazine.

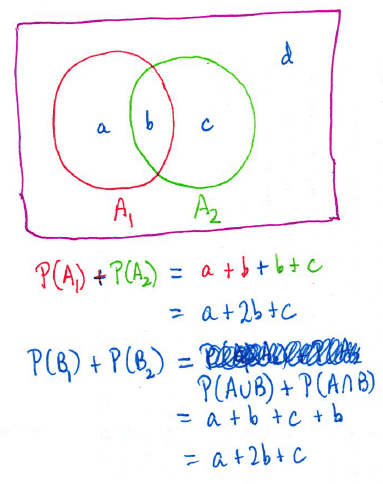
Let $A_1, \dots, A_n$ be arbitrary events in a probability field. Denote by $B_k$ the event that at least $k$ of $A_1, \dots A_n$ occur. Prove that $\displaystyle \sum_{k=1}^n P(B_k) = \sum_{k=1}^n P(A_k)$ .

I’ll admit when I first read this problem, I didn’t believe it. I had to draw a couple of Venn diagrams to convince myself that it actually worked:

Of course, pictures are not proofs, so I started giving the problem more thought.

I wish I could say where I got the inspiration from, but I got the idea to define a new random variable $N$ to be the number of events from $A_1, \dots A_n$ that occur. With this definition, $B_k$ becomes the event that $N \ge k$ , so that

$\displaystyle \sum_{k=1}^n P(B_k) = \sum_{k=1}^n P(N \ge k)$

At this point, my Spidey Sense went off: that’s the tail-sum formula for expectation! Since $N$ is a non-negative integer-valued random variable, the mean of $N$ can be computed by

$E(N) = \displaystyle \sum_{k=1}^n P(N \ge k)$ .

Said another way, $E(N) = \displaystyle \sum_{k=1}^n P(B_k)$ .

Therefore, to solve the problem, it remains to show that $\displaystyle \sum_{k=1}^n P(A_k)$ is also equal to $E(N)$ . To do this, I employed the standard technique from the bag of tricks of writing $N$ as the sum of indicator random variables. Define

$I_k = \displaystyle \bigg\{ \begin{array}{ll} 1, & A_k \hbox{~occurs} \\ 0, & A_k \hbox{~does not occur} \end{array}$

Then $N = I_1 + \dots + I_n$ , so that

$E(N) = \displaystyle \sum_{k=1}^n E(I_k) =\sum_{k=1}^n [1 \cdot P(A_k) + 0 \cdot P(A_k^c)] =\sum_{k=1}^n P(A_k)$ .

Equating the two expressions for $E(N)$ , we conclude that $\displaystyle \sum_{k=1}^n P(B_k) = \sum_{k=1}^n P(A_k)$ , as claimed.

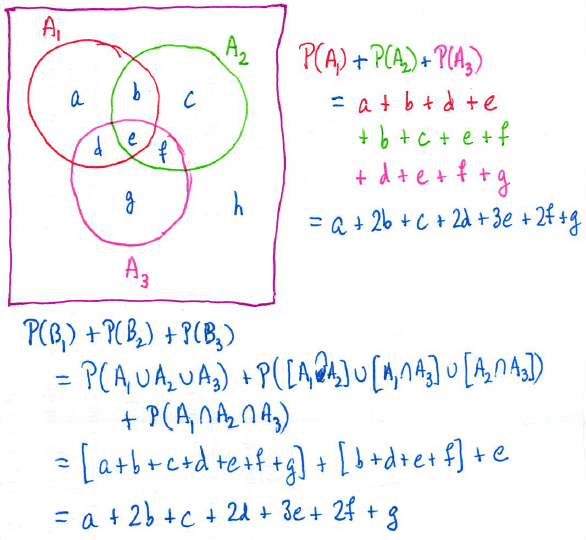
Solving Problems Submitted to MAA Journals (Part 4)

Published by John Quintanilla

Leave a comment Cancel reply

Share this:

Related

Published by John Quintanilla

Leave a comment Cancel reply