Inverse Functions: Arcsecant (Part 27)

We now turn to a little-taught and perhaps controversial inverse function: arcsecant. As we’ve seen throughout this series, the domain of this inverse function must be chosen so that the graph of $y = \sec x$ satisfies the horizontal line test. It turns out that the choice of domain has surprising consequences that are almost unforeseeable using only the tools of Precalculus.

The standard definition of $y = \sec^{-1} x$ uses the interval $[0,\pi]$ , so that

$\sec^{-1} x = \cos^{-1} \left( \displaystyle \frac{1}{x} \right)$

Why would this be controversial? Let’s fast-forward a couple of semesters and use implicit differentiation (see also https://meangreenmath.com/2014/08/08/different-definitions-of-logarithm-part-8/ for how this same logic is used for other inverse functions) to find the derivative of $y = \sec^{-1} x$ :

$x = \sec y$

$\displaystyle \frac{d}{dx} (x) = \displaystyle \frac{d}{dx} (\sec y)$

$1 = \sec y \tan y \displaystyle \frac{dy}{dx}$

$\displaystyle \frac{1}{\sec y \tan y} = \displaystyle \frac{dy}{dx}$

At this point, the object is to convert the left-hand side to something involving only $x$ . Clearly, we can replace $\sec y$ with $x$ . However, doing the same with $\tan y$ is trickier. We begin with one of the Pythagorean identities:

$1 + \tan^2 y = \sec^2 y$

$\tan^2 y = \sec^2 y - 1$

$\tan^2 y = x^2 - 1$

$\tan y = \sqrt{x^2 - 1} \qquad \hbox{or} \tan y = -\sqrt{x^2 - 1}$

So which is it, the positive answer or the negative answer? The answer is, without additional information, we don’t know!

If $0 \le y < \pi/2$ (so that $x = \sec y \ge 1$ ), then $\tan y$ is positive, and so $\tan y = \sqrt{\sec^2 y - 1}$ .
If $\pi/2 < y \le \pi$ (so that $x = \sec y \le 1$ ), then $\tan y$ is negative, and so $\tan y = -\sqrt{\sec^2 y - 1}$ .

We therefore have two formulas for the derivative of $y = \sec^{-1} x$ :

$\displaystyle \frac{d}{dx} sec^{-1} x = \displaystyle \frac{1}{x \sqrt{x^2-1}} \qquad \hbox{if} \qquad x > 1$

$\displaystyle \frac{d}{dx} sec^{-1} x = \displaystyle -\frac{1}{x \sqrt{x^2-1}} \qquad \hbox{if} \qquad x < 1$

These may then be combined into the single formula

$\displaystyle \frac{d}{dx} sec^{-1} x = \displaystyle \frac{1}{|x| \sqrt{x^2-1}}$

It gets better. Let’s now find the integral

$\displaystyle \int \frac{dx}{x \sqrt{x^2 -1}}$

Several calculus textbooks that I’ve seen will lazily give the answer

$\displaystyle \int \frac{dx}{x \sqrt{x^2 -1}} = \sec^{-1} x + C$

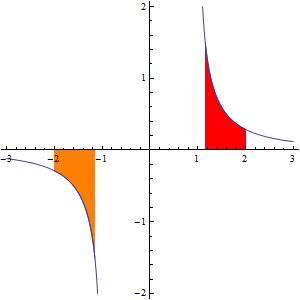
This answer works as long as $x > 1$ , so that $|x|$ reduces to simply $x$ . For example, the red signed area in the above picture on the interval $[2\sqrt{3}/3,2]$ may be correctly computed as

$\displaystyle \int_{2\sqrt{3}/3}^2 \frac{dx}{x \sqrt{x^2 -1}} = \sec^{-1} 2 - \sec^{-1} \displaystyle \frac{2\sqrt{3}}{3}$

$= \cos^{-1} \left( \displaystyle \frac{1}{2} \right) - \cos^{-1} \left( \displaystyle \frac{\sqrt{3}}{2} \right)$

$= \displaystyle \frac{\pi}{3} - \frac{\pi}{6}$

$= \displaystyle \frac{\pi}{6}$

However, the orange signed area on the interval $[-2,-2\sqrt{3}/3]$ is incorrectly computed using this formula!

$\displaystyle \int_{-2}^{-2\sqrt{3}/3} \frac{dx}{x \sqrt{x^2 -1}} = \sec^{-1} \left( - \displaystyle \frac{2\sqrt{3}}{3} \right) - \sec^{-1} (-2)$

$= \cos^{-1} \left( -\displaystyle \frac{\sqrt{3}}{2} \right) -\cos^{-1} \left( \displaystyle \frac{1}{2} \right)$

$= \displaystyle \frac{5\pi}{6} - \frac{2\pi}{3}$

$= \displaystyle \frac{\pi}{6}$

This is patently false, as the picture clearly indicates that the above integral has to be negative. For this reason, careful calculus textbooks will often ask students to solve a problem like

$\displaystyle \int \frac{dx}{x \sqrt{x^2 -1}}, \qquad x > 1$

and the caveat $x > 1$ is needed to ensure that the correct antiderivative is used. Indeed, a calculus textbook that doesn’t include such caveats are worthy of any scorn that an instructor cares to heap upon it.

Inverse Functions: Arcsecant (Part 27)

Published by John Quintanilla

Leave a comment Cancel reply

Share this:

Related

Published by John Quintanilla

Leave a comment Cancel reply