Engaging students: Introducing variables and expressions

In my capstone class for future secondary math teachers, I ask my students to come up with ideas for engaging their students with different topics in the secondary mathematics curriculum. In other words, the point of the assignment was not to devise a full-blown lesson plan on this topic. Instead, I asked my students to think about three different ways of getting their students interested in the topic in the first place.

I plan to share some of the best of these ideas on this blog (after asking my students’ permission, of course).

This student submission again comes from my former student Caitlin Kirk. Her topic, from Pre-Algebra: introducing variables and expressions.

To keep track of some of the coldest things in the universe, scientist use the Kelvin temperature scale that begins at 0 Kelvin, or Absolute Zero. Nothing can ever be colder than Absolute Zero because at this temperature, all motion stops. The table below shows some typical temperatures of different systems in the universe.

Table of Cold Places

Temp.(K)	Location
183	Vostok, Antarctica
160	Phobos- a moon of Mars
128	Europa in the summer
120	Moon at night
88	Miranda surface temp.
81	Enceladus in the summer
70	Mercury at night
55	Pluto in the summertime
50	Dwarf Planet Quaoar
33	Pluto in the wintertime
1	Boomerang Nebula
0	ABSOLUTE ZERO

You are probably already familiar with the Celsius (C) and Fahrenheit (F) temperature scales. The two formulas below show how to switch from degrees-C to degrees-F.

Because the Kelvin scale is related to the Celsius scale, we can also convert from Celsius to Kelvin (K) using the equation:

Problems

Use these three equations to convert between the three temperature scales:

Problem 1: 212 F converted to K

Problem 2: 0 K converted to F

Problem 3: 100 C converted to K

Problem 4: Two scientists measure the daytime temperature of the moon using two different instruments. The first instrument gives a reading of +107 C while the second instrument gives +221 F.

a. What are the equivalent temperatures on the Kelvin scale?

b. What is the average daytime temperature on the Kelvin scale?

Problem 5: Humans can survive without protective clothing in temperatures ranging from 0 F to 130 F. In what, if any, locations from the table above can humans survive?

Solutions

Problem 1: First convert to C:  C = 5/9 (212-32) = +100 C. Then convert from C to K: K = 273 + 100 = 373 Kelvin.

Problem 2: First convert to Celsius:    0 = 273 + C so C = -273. Then convert from C to F: F = 9/5 (-273) + 32 = -459 Fahrenheit.

Problem 3: K = 273 – 100 = 173 Kelvin.

Problem 4:

a. 107 C becomes K = 273 + 107 = 380 Kelvin.  221 F becomes C = 5/9(221-32) = 105 C, and so K = 273 + 105 = 378 Kelvin.

b. (380 + 378)/2 = 379 Kelvin

Problem 5:

First convert 0 F and 130 F to Celsius so that the conversion to Kelvin is quicker. 0 F becomes C = 5/9(0-32) = -18 C (rounded to the nearest degree) and 130 F becomes C = 5/9 (130-32) = 54 C (rounded to the nearest degree).

Next, convert -18 C and 54 C to Kelvin. -18 C becomes K = 273-18 = 255 and 54 C becomes k = 273 + 54 = 327 K.

None of the locations on the table have temperatures between 255 K and 327 K, therefore humans could not survive in any of these space locations.

A. How can this topic be used in your students’ future courses in mathematics or science?

This topic is one of the first experiences students have with algebra. Since algebra is the point from which students dive into more advanced mathematics, this topic will be used in many different areas of future mathematics. After mastering the use of one variable, with the basic operations of addition, subtraction, multiplication, and division, students will be introduced to the use of more than one variable. They may be asked to calculate the area of a solid whose perimeter is given and whose side lengths are unknown variables. Or in a more advanced setting, they may be asked to calculate how much money will be in a bank account after five years of interest compounded continuously. In fact, the use of variables is present and important in every mathematics class from Algebra I through Calculus and beyond. There very well may never be a day in a mathematics students’ life where they will not see a variable after variables have been introduced.

B.  How does this topic extend what your students should have learned in previous courses?

 In basic arithmetic, probably in elementary or early middle school math classes, students learn how to do calculations with numbers using the four basic operations of addition, subtraction, multiplication and division. They also learn simple applications of these basic operations by calculating the area and perimeter of a rectangle, for example. Introducing variables and expressions is a continuation of those same ideas except that one or more of the numbers is now an unknown variable. Students can rely on the arithmetic skills they already possess when learning this introduction to algebra with variables and expressions.

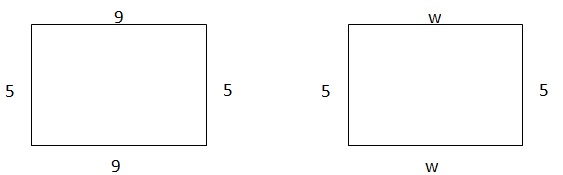
Students are familiar with calculating the area and perimeter of figures like the one on the left before they are introduced to variables. Later, they may see the same figure with the addition of a variable, as shown on the right. The addition of the variable will come with new instructions as well.

The difficulty of problems using variables is determined by the information given in the problems. For instance, the problem on the right can be a one step equation if an area and perimeter are given so that students only need to solve for w. The difficulty can be increased by giving only a perimeter so that students must solve for w and then for the area.